Advertisements
Advertisements
प्रश्न
Tamper-proof tetra-packed milk guarantees both freshness and security. This milk ensures uncompromised quality, preserving the nutritional values within and making it a reliable choice for health-conscious individuals.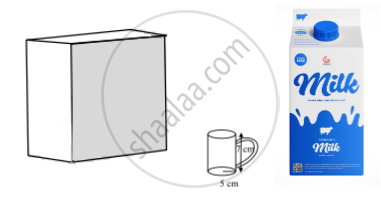
500 ml milk is packed in a cuboidal container of dimensions 15 cm × 8 cm × 5 cm. These milk packets are then packed in cuboidal cartons of dimensions 30 cm × 32 cm × 15 cm.
Based on the above-given information, answer the following questions:
i. Find the volume of the cuboidal carton. (1)
ii. a. Find the total surface area of the milk packet. (2)
OR
b. How many milk packets can be filled in a carton? (2)
iii. How much milk can the cup (as shown in the figure) hold? (1)
उत्तर
(i) Volume of the cuboidal carton
The formula for the volume of a cuboid is:
V = length × breadth × height
length = 30 cm, breadth = 32 cm, height = 15 cm
V = 30 × 32 × 15
V = 14400 cm3
(ii) a. Total Surface Area of the Milk Packet
TSA = 2(lb + bh + hl)
l = 15 cm, b = 8 cm, h = 5 cm
TSA = 2 × (15 × 8 + 8 × 5 + 5 × 15)
TSA = 2 × (120 + 40 + 75)
TSA = 2 × 235
TSA = 470 cm2
(ii) b. Number of Milk Packets in the Carton
Step 1: Volume of a single milk packet
V = l × b × h
V = 15 × 8 × 5
V = 600 cm3
Step 2: Number of packets
Number of packets = `"Volume of carton"/"Volume of one packet"`
= `14400/600`
= 24
(iii) Volume of the Cup
The given cup in the image is cylindrical. The volume of a cylinder is given by:
V = πr2h
From the image:
- Radius r = 5
- Height h is not provided in the image. To calculate the exact volume, we need the height of the cup.
APPEARS IN
संबंधित प्रश्न
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
Find the volume of a solid in the form of a right circular cylinder with hemi-spherical ends whose total length is 2.7 m and the diameter of each hemi-spherical end is 0.7 m.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
How many lead shots each 3 mm in diameter can be made from a cuboid of dimensions 9 cm × 11 cm × 12 cm ?
The total surface area of a solid hemisphere of radius 7 cm is ______.
