Advertisements
Advertisements
प्रश्न
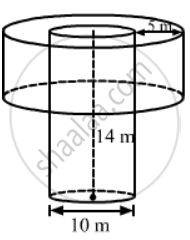
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
उत्तर
We have,
Radius of well, R = `10/2` = 5 m,
Depth of the well, H = 14 m and
Width of the embarkment = 5 m,
Also, the outer radius of the embankment, r = R + 5 = 5 + 5 = 10 m
And , the inner radius of the embarkment = R = 5m
Let the height of the embankment = 5 m,
Also, the outer radius of the embankment, r = R + 5 = 5 + 5 = 10 m
And, the inner radius of the embankment = R = 5 m
Let the height of the embarkment be h.
Now,
Volume of the embankment = Volume of the earth taken out
⇒ Volume of embankment = Volume of the well
⇒ (πr2 - πR2) h = πR2H
⇒ π (r2 - R2) h = πR2H
⇒ (r2 - R2) h = R2H
⇒ (102 - 52) h = 5 × 5 × 14
⇒ (100 - 25) h = 25 × 14
⇒ 75 h = 25 × 14
`⇒ "h" = (25xx14)/75 `
`therefore "h" = 14/3 "m"`
So, the height of the embankment is `14/3` m
Value: We must lanour hard to make maximum use of the available resources.
Disclaimer: The answer provided in the textbook is incorrect. It has been corrected above.
APPEARS IN
संबंधित प्रश्न
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
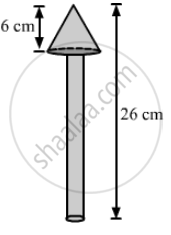
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
If the volumes of a cube is 1728 cm³, the length of its edge is equal to ______.
The curved surface area of glass having radii 3 cm and 4 cm respectively and slant height 10 cm is ______.
Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is 6πr2.
Statement A (Assertion): Total Surface area of the top is the sum of the curved surface area of the hemisphere and the curved surface area of the cone.
Statement R( Reason): Top is obtained by joining the plane surfaces of the hemisphere and cone together.

