Advertisements
Advertisements
प्रश्न
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
उत्तर
No. of cones = 504
Diameter of a cone = 3.5 cm
Radius of the cone, r = 1.75 cm
Height of the cone, h = 3 cm
Volume of a cone
`=1/3pir^2h`
`=1/3xxpixx(3.5/2)^2xx3`
`=1/3xxpixx3.5/2xx3.5/2xx3 " cm"^2`
Volume of 504 cones
`=504xx1/3xxpixx3.5/2xx3.5/2xx3 " cm"^2`
Let the radius of the new sphere be ‘R’.
Volume of the sphere `=4/3 pir^3 `
Volume of 504 cones = Volume of the sphere
`504xx1/3xxpixx3.5/2xx3.5/2xx3=4/3 piR^3`
`(504xx1xxpixx3.5xx3.5xx3xx3)/(3xx2xx2xx4xxpi)=R^3`
`R^3=(504xx3xx49)/64`
`R^3=(8xx27xx7^3)/64`
`R=(2xx3xx7)/4`
`R=21/2=10.5 cm`
Radius of the new sphere = 10.5 cm
APPEARS IN
संबंधित प्रश्न
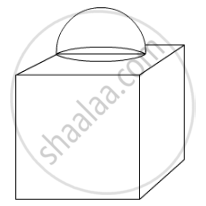
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. [Use `pi = 22/7`]
A tent of height 77dm is in the form a right circular cylinder of diameter 36m and height 44dm surmounted by a right circular cone. Find the cost of canvas at Rs.3.50 per m2 ?
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
Two solid cones A and B are placed in a cylindrical tube as shown in fig .16.76. The ratio of their capacities are 2: 1 . Find the heights and capacities of the cones . Also, find the volume of the remaining portion of the cylinder.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, the total area of the canvas required in m2 is
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
A right triangle whose sides are 15 cm and 20 cm (other than hypotenuse), is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)
