Advertisements
Advertisements
प्रश्न
Two solid cones A and B are placed in a cylindrical tube as shown in fig .16.76. The ratio of their capacities are 2: 1 . Find the heights and capacities of the cones . Also, find the volume of the remaining portion of the cylinder.
उत्तर
V1 : V2 = 2 : 1
Diameter of the cylinder = 6 cm
Radius, r = 3 cm
Height of the cylinder = 21 cm
Let the height of one cone be H.
So, the height of the other cone will be 21 − H.
\[\frac{V_1}{V_2} = \frac{\pi \left( 3 \right)^2 H}{\pi \left( 3 \right)^2 \left( 21 - H \right)}\]
\[ \Rightarrow \frac{2}{1} = \frac{H}{21 - H}\]
\[ \Rightarrow 42 - 2H = H\]
\[ \Rightarrow H = 14 cm\]
Height of one of the cones will be 14 cm and of the other will be 21 − H = 21 − 14 = 7 cm
Volume of cone with height 14 cm = \[V_1 = \pi \left( 3 \right)^2 \times 14 = 396 {cm}^3\]
Volume of cone with height 7 cm = \[V_2 = \frac{1}{3}\pi \left( 3 \right)^2 \times 7 = 66 {cm}^3\]
Volume of the remaining portion of the cylinder =
\[\text { Volume of the cylinder - volume of cone 1 - volume of cone 2 }\]
\[\Rightarrow V = \pi \left( 3 \right)^2 \times 21 - 396 - 66\]
\[ = 594 - 396 - 66\]
\[ = 132 {cm}^3\]
APPEARS IN
संबंधित प्रश्न
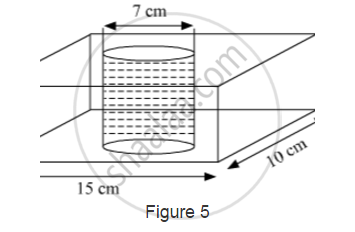
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
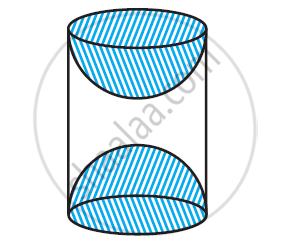
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
From a solid right circular cylinder of height 2.4 cm and radius 0.7 cm, a right circular cone of same height and same radius is cut out. Find the total surface area of the remaining solid.
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
A solid sphere of radius 'r' is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm, find the value of 'r'.
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, then find the cost of painting the toy at the rate of 70 paise per sq cm.
A plumbline (sahul) is a combination of
Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is 6πr2.
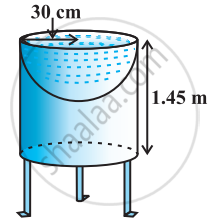
Ramesh made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.