Advertisements
Advertisements
Question
Two solid cones A and B are placed in a cylindrical tube as shown in fig .16.76. The ratio of their capacities are 2: 1 . Find the heights and capacities of the cones . Also, find the volume of the remaining portion of the cylinder.
Solution
V1 : V2 = 2 : 1
Diameter of the cylinder = 6 cm
Radius, r = 3 cm
Height of the cylinder = 21 cm
Let the height of one cone be H.
So, the height of the other cone will be 21 − H.
\[\frac{V_1}{V_2} = \frac{\pi \left( 3 \right)^2 H}{\pi \left( 3 \right)^2 \left( 21 - H \right)}\]
\[ \Rightarrow \frac{2}{1} = \frac{H}{21 - H}\]
\[ \Rightarrow 42 - 2H = H\]
\[ \Rightarrow H = 14 cm\]
Height of one of the cones will be 14 cm and of the other will be 21 − H = 21 − 14 = 7 cm
Volume of cone with height 14 cm = \[V_1 = \pi \left( 3 \right)^2 \times 14 = 396 {cm}^3\]
Volume of cone with height 7 cm = \[V_2 = \frac{1}{3}\pi \left( 3 \right)^2 \times 7 = 66 {cm}^3\]
Volume of the remaining portion of the cylinder =
\[\text { Volume of the cylinder - volume of cone 1 - volume of cone 2 }\]
\[\Rightarrow V = \pi \left( 3 \right)^2 \times 21 - 396 - 66\]
\[ = 594 - 396 - 66\]
\[ = 132 {cm}^3\]
APPEARS IN
RELATED QUESTIONS
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is:
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
Find the number of metallic circular discs with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm .
The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, the total area of the canvas required in m2 is
How many cubes of 10 cm edge can be put in a cubical box of 1 m edge?
How many lead shots each 3 mm in diameter can be made from a cuboid of dimensions 9 cm × 11 cm × 12 cm ?
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
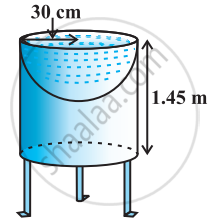
Ramesh made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.