Advertisements
Advertisements
Question
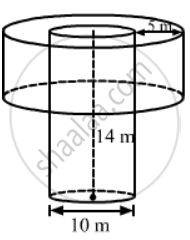
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
Advertisements
Solution
We have,
Radius of well, R = `10/2` = 5 m,
Depth of the well, H = 14 m and
Width of the embarkment = 5 m,
Also, the outer radius of the embankment, r = R + 5 = 5 + 5 = 10 m
And , the inner radius of the embarkment = R = 5m
Let the height of the embankment = 5 m,
Also, the outer radius of the embankment, r = R + 5 = 5 + 5 = 10 m
And, the inner radius of the embankment = R = 5 m
Let the height of the embarkment be h.
Now,
Volume of the embankment = Volume of the earth taken out
⇒ Volume of embankment = Volume of the well
⇒ (πr2 - πR2) h = πR2H
⇒ π (r2 - R2) h = πR2H
⇒ (r2 - R2) h = R2H
⇒ (102 - 52) h = 5 × 5 × 14
⇒ (100 - 25) h = 25 × 14
⇒ 75 h = 25 × 14
`⇒ "h" = (25xx14)/75 `
`therefore "h" = 14/3 "m"`
So, the height of the embankment is `14/3` m
Value: We must lanour hard to make maximum use of the available resources.
Disclaimer: The answer provided in the textbook is incorrect. It has been corrected above.
RELATED QUESTIONS
A right circular cone of radius 3 cm, has a curved surface area of 47.1 cm2. Find the volume of the cone. (use π 3.14).
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is 10459 `3/7` cm3. The radii of its lower and upper circular ends are 8cm and 20cm. find the cost of metal sheet used in making container at rate of Rs 1.4 per cm2?
In Figure 4, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region.\[[Use\pi = 3 . 14]\]
A vessel is in the form of hemispherical bowl surmounted by a hollow cylinder of same diameter. The diameter of the hemispherical bowl is 14 cm and the total height of the vessel is 13 cm. Find the total surface area of the vessel. `[\text{Use}pi=22/7]`
Three solid spheres of radii 3, 4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is
A rocket is in the form of a circular cylinder closed at the lower end and a cone of the same radius is attached to the top. The radius of the cylinder is 2.5 m, its height is 21 m and the slant height of the cone is 8 m. Calculate the total surface area of the rocket.
A solid metallic sphere of diameter 21 cm is melted and recast into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.
How many lead shots each 3 mm in diameter can be made from a cuboid of dimensions 9 cm × 11 cm × 12 cm ?
The total surface area of a solid hemisphere of radius r is ________.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
The total surface area of a solid hemisphere of radius 7 cm is ______.
Ramesh made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.
The ratio of total surface area of a solid hemisphere to the square of its radius is ______.
