Advertisements
Advertisements
Question
A right triangle whose sides are 15 cm and 20 cm (other than hypotenuse), is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)
Solution
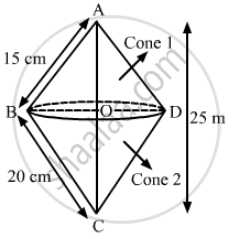
We have,
In ΔABC, ∠B = 90° , AB = l1 =15 cm and BC = l2 = 20 cm
Let OD = OB = r , AO = h1 and CO = h2
Using Pythagoras therom,
`"AC" = sqrt("AB"^2 + "BC"^2)`
`=sqrt(15^2 + 20^2)`
`= sqrt(225 + 400)`
`= sqrt(625)`
⇒ h = 25 cm
As, ar(ΔABC)` = 1/2xxACxxBO=1/2xxABxxBC `
⇒ AC × BO = AB × BC
⇒ 25r = 15 × 20
`rArr r = (15xx20)/25`
⇒ r = 12 cm
Now,
Volume of the double cone so formed = Volume of cone 1 +Volume of cone 2
`= 1/3 pir^2h_1 + 1/3pir^2h_2`
`= 1/3 pir^2 ("h"_1 + "h"_2)`
`= 1/3pi"r"^2"h"`
`= 1/3xx3.14xx12xx12xx25`
= 3768 cm3
Also,
surace area of the solid so formed = CAS of cone 1 + CSA of cone 2
= πrl1 + πrl2
= πr ( l1 + l2 )
`= 22/7xx12xx(15+20)`
`=22/7xx12xx35`
= 1320 cm2
APPEARS IN
RELATED QUESTIONS
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs. 5 per 100 sq. cm. [Use π = 3.14]
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
Three solid spheres of radii 3, 4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
From a cubical piece of wood of side 21 cm, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece. Find the surface area and volume of the remaining piece.
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
The curved surface area of glass having radii 3 cm and 4 cm respectively and slant height 10 cm is ______.
The total surface area of a solid hemisphere of radius 7 cm is ______.
