Advertisements
Advertisements
प्रश्न
A right triangle whose sides are 15 cm and 20 cm (other than hypotenuse), is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)
Advertisements
उत्तर
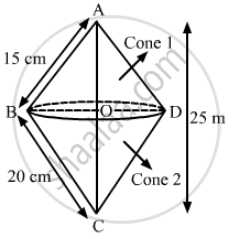
We have,
In ΔABC, ∠B = 90° , AB = l1 =15 cm and BC = l2 = 20 cm
Let OD = OB = r , AO = h1 and CO = h2
Using Pythagoras therom,
`"AC" = sqrt("AB"^2 + "BC"^2)`
`=sqrt(15^2 + 20^2)`
`= sqrt(225 + 400)`
`= sqrt(625)`
⇒ h = 25 cm
As, ar(ΔABC)` = 1/2xxACxxBO=1/2xxABxxBC `
⇒ AC × BO = AB × BC
⇒ 25r = 15 × 20
`rArr r = (15xx20)/25`
⇒ r = 12 cm
Now,
Volume of the double cone so formed = Volume of cone 1 +Volume of cone 2
`= 1/3 pir^2h_1 + 1/3pir^2h_2`
`= 1/3 pir^2 ("h"_1 + "h"_2)`
`= 1/3pi"r"^2"h"`
`= 1/3xx3.14xx12xx12xx25`
= 3768 cm3
Also,
surace area of the solid so formed = CAS of cone 1 + CSA of cone 2
= πrl1 + πrl2
= πr ( l1 + l2 )
`= 22/7xx12xx(15+20)`
`=22/7xx12xx35`
= 1320 cm2
APPEARS IN
संबंधित प्रश्न
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. `("use " pi=22/7)`
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid [take π=22/7]
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy [Use π =`22/7`]
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m2.
(Note that the base of the tent will not be covered with canvas.) [Use `pi = 22/7`]
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
In Figure 4, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region.\[[Use\pi = 3 . 14]\]
From a solid cube of side 7 cm , a conical cavity of height 7 cm and radius 3 cm is hollowed out . Find the volume of the remaining solid.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
A rocket is in the form of a circular cylinder closed at the lower end and a cone of the same radius is attached to the top. The radius of the cylinder is 2.5 m, its height is 21 m and the slant height of the cone is 8 m. Calculate the total surface area of the rocket.
A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, then find the cost of painting the toy at the rate of 70 paise per sq cm.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
From a cubical piece of wood of side 21 cm, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece. Find the surface area and volume of the remaining piece.
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm, respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.
In a right circular cone, the cross-section made by a plane parallel to the base is a
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14)
If two solid hemispheres of the same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
