Advertisements
Advertisements
प्रश्न
A right triangle whose sides are 15 cm and 20 cm (other than hypotenuse), is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)
उत्तर
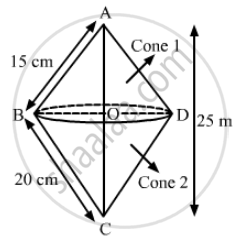
We have,
In ΔABC, ∠B = 90°, AB = l1 = 15 cm and BC = l2 = 20
Let OD = OB = r , AO = h1 and CO = h2
Using Pythagoras theorem,
` "AC" =sqrt("AB"^2 + "BC"^2 )`
`= sqrt(15^2 + 20^2)`
`=sqrt(225 + 400)`
` =sqrt(625)`
⇒ h = 25 cm
`"As, ar"(Delta "ABC") = 1/2xx"AC"xx"BO" = 1/2xx"AB"xx"BC"`
⇒ AC × BO = AB × BC
⇒ 25r = 15 × 20
`rArr r = (15xx20)/25`
⇒ r = 12 cm
Now,
Volume of the double cone so formed = Volume of cone 1 + Volume of cone 2
`= 1/3pi"r"^2"h"_1 + 1/3pi"r"^2"h"_2`
`=1/3pir^2(h_1 + h_2)`
`= 1/3pi"r"^2"h"`
`= 1/3xx3.14xx12xx12xx25`
= 3768 cm3
Also,
Surace of the solid so formed = CAS of cone 1 + CSA of cone 2
= πrl1 +πrl2
= πr ( l1 + l2 )
`= 22/7 xx 12 xx (15+20)`
`= 22/7xx12xx35`
= 1320 cm2
APPEARS IN
संबंधित प्रश्न
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
The surface area of a sphere is 616 cm2 . Find its radius.
Assertion (A)
The curved surface area of a cone of base radius 3 cm and height 4 cm is 15π cm2.\
Reason (R)
Volume of a cone = πr2h
- Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
The dimensions of a metallic cuboid are 44 cm × 42 cm × 21 cm. it is molten and recast into a sphere. Find the surface area of the sphere.
Arrange the given objects according to their volume
The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. The curved surface area of the bucket is ______.
If R is the radius of the base of the hat, then the total outer surface area of the hat is ______.

______ of a solid is the measurement of the space occupied by it.
If the length of the diagonal of a cube is `5sqrt(3)` cm, find the total surface area.
Length of the diagonal of the cube = `square`
So, `square` = `5sqrt(3)`
⇒ Side = `square`
Total surface area of cube = `square`
= `square` × `square` × `square`
= `square` cm2
Hence, the total surface area is `square`.
