Question

A right triangle whose sides are 15 cm and 20 cm (other than hypotenuse), is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)

Answer 1

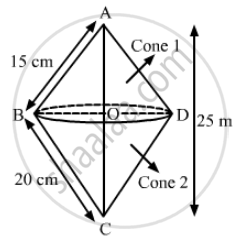
We have,

In ΔABC, ∠B = 90°, AB = l₁ = 15 cm and  BC = l2 = 20

Let OD = OB = r , AO = h₁ and CO = h₂

Using Pythagoras theorem,

` "AC" =sqrt("AB"^2 + "BC"^2 )`

       `= sqrt(15^2 + 20^2)`

      `=sqrt(225 + 400)`

     ` =sqrt(625)`

⇒ h = 25 cm

`"As, ar"(Delta "ABC") = 1/2xx"AC"xx"BO" = 1/2xx"AB"xx"BC"`

⇒ AC × BO = AB × BC

⇒ 25r = 15 × 20 

`rArr r = (15xx20)/25`

⇒ r = 12 cm

Now,

Volume of the double cone so formed = Volume of cone 1 + Volume of cone 2

`= 1/3pi"r"^2"h"_1 + 1/3pi"r"^2"h"_2`

`=1/3pir^2(h_1 + h_2)`

`= 1/3pi"r"^2"h"`

`= 1/3xx3.14xx12xx12xx25`

= 3768 cm³ 

Also,

Surace of the solid so formed = CAS of cone 1 + CSA of cone 2

= πrl₁ +πrl₂

= πr ( l₁ + l₂ )

`= 22/7 xx 12 xx (15+20)`

`= 22/7xx12xx35`

= 1320 cm²