Advertisements
Advertisements
प्रश्न
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
उत्तर
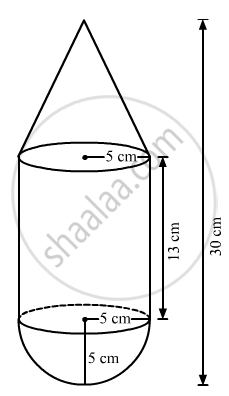
S1 = 2π(2)(13)
S1 =408.2cm2
Curved surface area of cone(S1) = πrl
Let l be slant height of cone
`l=sqrt(r^2+h^2`
h = 30 - 13 - 5 = 12cm
⇒`l=sqrt(12^2+5^2)` = 13cm
l = 13cm
∴Curved surface area of cone(S2) = π(5)(13)
= 204.1cm2
Curved surface area of hemisphere(S3) = 2πr2
= 2π(5)2
= 2π(25) = 50π = 157cm2
Total curved surface area(S) = S1 + S2 + S3
S = 408.2 + 204.1 + 157
S = 769.3cm2
∴ Surface area of toy(S) = 769.3cm2
APPEARS IN
संबंधित प्रश्न
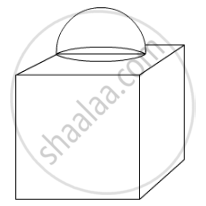
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Radii of circular ends of a solid frustum off a cone re 33cm and 27cm and its slant height are 10cm. find its total surface area?
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
From a cubical piece of wood of side 21 cm, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece. Find the surface area and volume of the remaining piece.
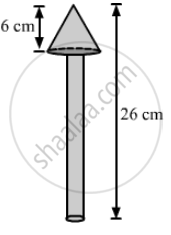
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
A solid metallic sphere of diameter 21 cm is melted and recast into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14)
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
There are two identical solid cubical boxes of side 7 cm. From the top face of the first cube a hemisphere of diameter equal to the side of the cube is scooped out. This hemisphere is inverted and placed on the top of the second cube’s surface to form a dome. Find
- the ratio of the total surface area of the two new solids formed
- volume of each new solid formed.
