Advertisements
Advertisements
प्रश्न
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
उत्तर
Let the radius of the hemisphere be r units.
Volume of a hemisphere = Surface area of the hemisphere
\[\Rightarrow \frac{2}{3}\pi r^3 = 3\pi r^2 \]
\[ \Rightarrow \frac{2}{3}r = 3\]
\[ \Rightarrow r = \frac{9}{2}\]
\[ \Rightarrow d = 9 \text { units }\]
Hence, diameter of the hemisphere is equal to 9 units.
APPEARS IN
संबंधित प्रश्न
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs. 5 per 100 sq. cm. [Use π = 3.14]
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid [take π=22/7]
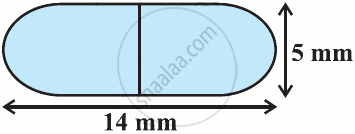
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
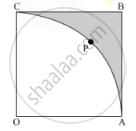
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of ₹5 per 100 sq cm. [Use ππ = 3.14]
Match the following columns:
| Column I | Column II |
| (a) The radii of the circular ends of a bucket, in the form of the frustum of a cone of height 30 cm, are 20 cm and 10 cm respectively. The capacity of the bucket is ........cm3. |
(p) 2418π |
| (b) The radii of the circular ends of a conical bucket of height 15 cm are 20 and 12 cm respectively. The slant height of the bucket is ........ cm. |
(q) 22000 |
| (c) The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. The total surface area of the bucket is .........cm2. |
(r) 12 |
| (d) Three solid metallic spheres of radii 3 cm, 4 cm and 5 cm are melted to form a single solid sphere. The diameter of the resulting sphere is ........ cm. |
(s) 17 |
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14)
Eight solid sphere of same size are made by melting a solid metallic cylinder of base diameter 6 cm and height 32 cm. The diameter of each sphere is ______.
