Advertisements
Advertisements
प्रश्न
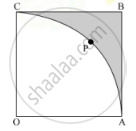
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
उत्तर
It is given that OABC is a square of side 7 cm.
∴ Area of square OABC = (7)2 cm2 = 49 cm2
Also, it is given that OAPC is a quadrant of circle with centre O.
∴Radius of the quadrant of the circle = OA = 7 cm
∴ Area of the quadrant of circle `1/4(pi^2)`
`=1/4(pixx7^2)cm^2`
`=(49pi)/4cm^2`
`=49/4xx22/7 cm^2`
`=77/2cm^2`
∴Area of the shaded region = Area of Square − Area of Quadrant of circle.
`=[49-77/2]cm^2`
`=[(98-77)/2]cm^2`
`=21/2cm^2`
`=10.5cm^2`
Thus, the area of the shaded region is 10.5 cm2.
संबंधित प्रश्न
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
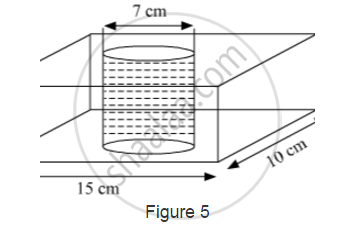
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
If the radii of circular ends of a bucket 24cm high are 5cm and 15cm. find surface area of
bucket?
A solid sphere of radius 'r' is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm, find the value of 'r'.
A solid metallic sphere of diameter 21 cm is melted and recast into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.
If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio ______.
The radius of spherical balloon increases from 8 cm to 12 cm. The ratio of the surface areas of balloon in two cases is ______.
Eight solid sphere of same size are made by melting a solid metallic cylinder of base diameter 6 cm and height 32 cm. The diameter of each sphere is ______.
There are two identical solid cubical boxes of side 7 cm. From the top face of the first cube a hemisphere of diameter equal to the side of the cube is scooped out. This hemisphere is inverted and placed on the top of the second cube’s surface to form a dome. Find
- the ratio of the total surface area of the two new solids formed
- volume of each new solid formed.
