Advertisements
Advertisements
рдкреНрд░рд╢реНрди
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
рдЙрддреНрддрд░
Internal diameter of the bowl = 36 cm
Internal radius of the bowl, r = 18 cm
Volume of the liquid, V =(2/3)ЁЭЬЛr3 =(2/3)× ЁЭЬЛ × 183
Let the height of the small bottle be ‘h’.
Diameter of a small cylindrical bottle = 6 cm
Radius of a small bottle, R = 3 cm
Volume of a single bottle = ЁЭЬЛR2h = ЁЭЬЛ × 32 × h
No. of small bottles, n = 72
Volume wasted in the transfer =(10/100)×(2/3)× ЁЭЬЛ × 183
Volume of liquid to be transferred in the bottles
`=2/3xxpixx18^3-10/100xx2/3xxpixx18^3`
`=2/3xxpixx18^3(1-10/100)`
`=2/3xxpixx18^3xx90/100`
we know that volume of cylinder =`pir^2h` so we get
`72(pir^2h)=(2/3xxpixx18^3xx90/100)`
`72=(2/3xxpixx18^3xx90/100)/(pixx3^2xxh)`
`72=(2/3xx18^3xx9/10)/(3^2xxh)`
`h=(2/3xxpixx18xx18xx18xx9/10)/(pixx3^2xx72) `
h=5.4 cm
Height of the small cylindrical bottle = 5.4 cm
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A rocket is in the form of a circular cylinder closed at the lower end and a cone of the same radius is attached to the top. The radius of the cylinder is 2.5 m, its height is 21 m and the slant height of the cone is 8 m. Calculate the total surface area of the rocket.
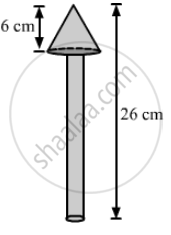
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
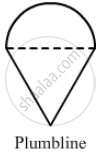
A plumbline (sahul) is a combination of
A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of тВ╣ 50 per litre. Also find the cost of metal sheet used to make the container, if it costs тВ╣ 10 per 100 cm2. (Take π = 3⋅14)
The total surface area of a solid hemisphere of radius r is ________.
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
3 cubes each of 8 cm edge are joined end to end. Find the total surface area of the cuboid.
