Advertisements
Advertisements
प्रश्न
A rocket is in the form of a circular cylinder closed at the lower end and a cone of the same radius is attached to the top. The radius of the cylinder is 2.5 m, its height is 21 m and the slant height of the cone is 8 m. Calculate the total surface area of the rocket.
उत्तर
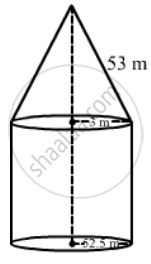
Radius of the cylinder = 2.5 m
Height of the cylinder = 21 m
Curved surface area of the cylinder `= 2pirh = 2xx22/7xx2.5xx21=330` m2
Radius of the cone = 2.5 m
Slant height of the cone = 8 m
Curved surface area of the cone `= pirl = 22/7 xx2.5xx8 = 62.86` m2
Area of circular base = `pir^2 = 22/7xx2.5xx2.5xx=19.643`
∴ Total surface area of rocket = 330 + 62.86 + 19.643 m2
APPEARS IN
संबंधित प्रश्न
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
Water in a canal, 5·4 m wide and 1·8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is 108 cm and the diameter of the cylinder is 36 cm, find the cost of polishing the surface at the rate of 7 paise per cm2 .
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm, respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.
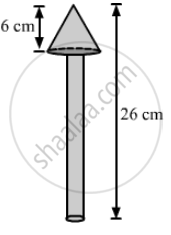
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is ______.

The curved surface area of glass having radii 3 cm and 4 cm respectively and slant height 10 cm is ______.
Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is 6πr2.
There are two identical solid cubical boxes of side 7 cm. From the top face of the first cube a hemisphere of diameter equal to the side of the cube is scooped out. This hemisphere is inverted and placed on the top of the second cube’s surface to form a dome. Find
- the ratio of the total surface area of the two new solids formed
- volume of each new solid formed.
