Advertisements
Advertisements
प्रश्न
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs. 5 per 100 sq. cm. [Use π = 3.14]
उत्तर
Side of the cubical block, a = 10 cm
Longest diagonal of the cubical block = a√3 = 10√3 cm
Since the cube is surmounted by a hemisphere, therefore the side of the cube should be equal to the diameter of the hemisphere.
Diameter of the sphere = 10 cm
Radius of the sphere, r = 5 cm
Total surface area of the solid = Total surface area of the cube – Inner cross-section area of the hemisphere + Curved surface area of the hemisphere
`=6a^2-pir^2+2pir^2`
`=6a^2+pir^2`
`=6xx(10)^2+3.14xx5^2`
`=600+78.5=678.5 cm^2`
Total surface area of the solid = 678.5 cm2
Cost of painting 100 cm2 = Rs. 5
Cost of painting 1 cm2 = Rs.5/100
Cost of painting the total surface area of the solid =(5/100)× 678.5 = Rs. 33.925 ≈ Rs. 34.
APPEARS IN
संबंधित प्रश्न
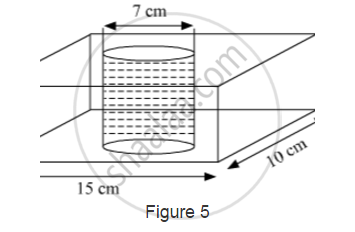
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
Water in a canal, 5·4 m wide and 1·8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
A frustum of a right circular cone has a diameter of base 20 cm, of top 12 cm, and height 3 cm. Find the area of its whole surface and volume.
A cylindrical tub, whose diameter is 12 cm and height 15 cm is full of ice-cream. The whole ice-cream is to be divided into 10 children in equal ice-cream cones, with conical base surmounted by hemispherical top. If the height of conical portion is twice the diameter of base, find the diameter of conical part of ice-cream cone ?
The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4 \[\frac{2}{3}\] cm and height 3 cm. Find the number of cones so formed.
The radius of spherical balloon increases from 8 cm to 12 cm. The ratio of the surface areas of balloon in two cases is ______.
The boilers are used in thermal power plants to store water and then used to produce steam. One such boiler consists of a cylindrical part in middle and two hemispherical parts at its both ends.
Length of the cylindrical part is 7 m and radius of cylindrical part is `7/2` m.
Find the total surface area and the volume of the boiler. Also, find the ratio of the volume of cylindrical part to the volume of one hemispherical part.

The ratio of total surface area of a solid hemisphere to the square of its radius is ______.
