Advertisements
Advertisements
प्रश्न
A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10 cm. and 6 cm, respectively. Find the total surface area of the solid. (Use π =`22/7`)
उत्तर
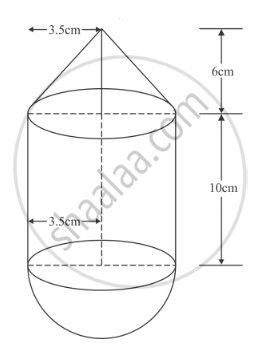
Given,
Radius of the common base(r) = 3.5 cm
Height of the cylindrical part (h) = 10 cm
Height of the conical part (H) = 6 cm
Let 'l' be the slant height of the cone
Then, we know that,
I2 = r2 + H2
I2 = 3.52 + 62
= 12.25 + 36
= 48.25
l = 6.95 cm
So, the curved surface area of the cone (S1) = πrl
S1 = π(3.5)(6.95)
S1 = `22/7 xx 3.5 xx 6.95`
S1 = 76.45 cm2
Curved surface area of cylinder (S2) = 2πrh
S2 = 2π(3.5)(10)
S2 = `2 xx 22/7 xx 3.5 xx 10`
S2 = 220 cm2
Curved surface area of hemisphere(S3) = 2πr2
S3 = `2 xx 22/7 xx 3.5^2`
S3 = 77 cm2
Total surface area of the solid is given by
S = S1 + S2 +S3
= 76.45 + 220 + 77
= 373.45 cm2
संबंधित प्रश्न
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
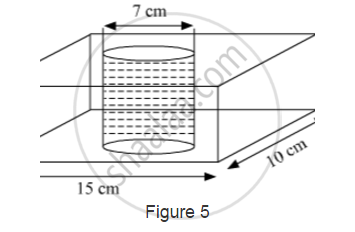
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
Radii of circular ends of a solid frustum off a cone re 33cm and 27cm and its slant height are 10cm. find its total surface area?
Three solid spheres of radii 3, 4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A hemispherical bowl of internal diameter 30 cm contains some liquid. This liquid is to be poured into cylindrical bottles of diameter 5 cm and height 6 cm each. Find the number of bottles required.
Match the following columns:
| Column I | Column II |
| (a) The radii of the circular ends of a bucket, in the form of the frustum of a cone of height 30 cm, are 20 cm and 10 cm respectively. The capacity of the bucket is ........cm3. |
(p) 2418π |
| (b) The radii of the circular ends of a conical bucket of height 15 cm are 20 and 12 cm respectively. The slant height of the bucket is ........ cm. |
(q) 22000 |
| (c) The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. The total surface area of the bucket is .........cm2. |
(r) 12 |
| (d) Three solid metallic spheres of radii 3 cm, 4 cm and 5 cm are melted to form a single solid sphere. The diameter of the resulting sphere is ........ cm. |
(s) 17 |
The total surface area of a solid hemisphere of radius r is ________.
