Advertisements
Advertisements
प्रश्न
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
उत्तर
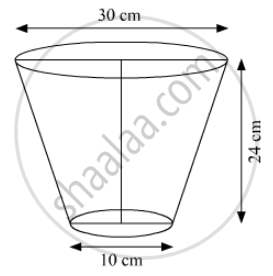
We have:
A radius of the upper end of the frustum, R = 15 cm; Radius of the lower end of the frustum, r = 5 cm; Height of frustum, h = 24 cm
we know
Slant height, `l^2 = h^2 + (R - r)^2`
`=> l^2 = ((24)^2 + (15 - 5)^2) = (576 + 100) = 676`
`= l = 26 cm`
1) Required area of the metal sheet = `pi[r^2 + 1(R + r)]` sq. cm
`= 3.14 [5^2 + 26(15 + 5)] cm^2`
`= 3.14 xx (25 + 520) cm^2`
`= 3.14 xx 545 cm^2`
`= 1711.3 cm^3`
2) Plastic is harmful to the environment and to protect the environment its use should be avoided.
APPEARS IN
संबंधित प्रश्न
In Fig. 4, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use `pi=22/7` and `sqrt5=2.236`)

The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
A solid sphere of radius 'r' is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm, find the value of 'r'.
A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, then find the cost of painting the toy at the rate of 70 paise per sq cm.
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of ₹ 50 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 10 per 100 cm2. (Take π = 3⋅14)
In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is ______.

If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
The total surface area of a solid hemisphere of radius 7 cm is ______.
