Advertisements
Advertisements
प्रश्न
The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
उत्तर
Inner radius of hollow cylinder r1 = 15 cm
Outer radius of hollow cylinder r2 = 20 cm
The volume of hollow cylinder `= pi (r_2^2 - r_1^2) h`
Since,
The hollow cylinder is melted and recast into a solid cylinder of same height.
Let r be the radius of solid cylinder.
Therefore,
The volume of solid cylinder = volume of hollow cylinder.
`pir^2 h = pi (r_2^2 - r_1^2) h`
`r^2 = (20^2 - 15^2)`
`r^2 = 35 xx 5`
`r = 13.2 cm`
Hence, the radius of solid cylinder is13.2 cm .
APPEARS IN
संबंधित प्रश्न
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
If the total surface area of a solid hemisphere is 462 cm2 , find its volume.[Take π=22/7]
The largest possible sphere is carved out of a wooden solid cube of side 7 em. Find the volume of the wood left. (Use\[\pi = \frac{22}{7}\]).
150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel.
A right circular cone of radius 3 cm, has a curved surface area of 47.1 cm2. Find the volume of the cone. (use π 3.14).
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. [Use `pi = 22/7`]
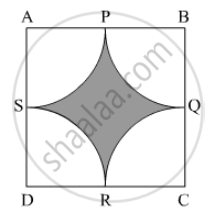
Find the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
The volume of a hemisphere is 2425 `1/2` cm3 . Find its curved surface area.
A solid metallic sphere of diameter 21 cm is melted and recast into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.
