Advertisements
Advertisements
Question
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
Solution
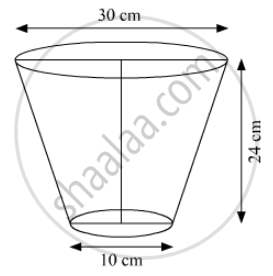
We have:
A radius of the upper end of the frustum, R = 15 cm; Radius of the lower end of the frustum, r = 5 cm; Height of frustum, h = 24 cm
we know
Slant height, `l^2 = h^2 + (R - r)^2`
`=> l^2 = ((24)^2 + (15 - 5)^2) = (576 + 100) = 676`
`= l = 26 cm`
1) Required area of the metal sheet = `pi[r^2 + 1(R + r)]` sq. cm
`= 3.14 [5^2 + 26(15 + 5)] cm^2`
`= 3.14 xx (25 + 520) cm^2`
`= 3.14 xx 545 cm^2`
`= 1711.3 cm^3`
2) Plastic is harmful to the environment and to protect the environment its use should be avoided.
APPEARS IN
RELATED QUESTIONS
Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs Rs. 100 per sq. m, find the amount, the associations will have to pay. What values are shown by these associations? [Use π=22/7]
A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the top (Use π = 22/7)
If the radii of circular ends of a bucket 24cm high are 5cm and 15cm. find surface area of
bucket?
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is:
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of these balls are 1.5 cm and 2 cm. Find the radius of the third ball.
