Advertisements
Advertisements
प्रश्न
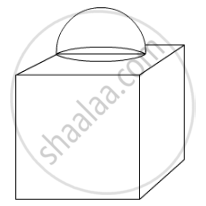
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
उत्तर

Surface area of the block = Total surface area of the cube − Base area of the hemisphere + Curved surface area of the hemisphere
=6×(Edge)2−πr2+2πr2
=(63+πr2)
`=(216+22/7xx3.5/2xx3.5/2)`
=(216+9.625)
=225.625 cm2
APPEARS IN
संबंधित प्रश्न
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/h. How much area will it irrigate in 10 minutes, if 8 cm of standing water is needed for irrigation?
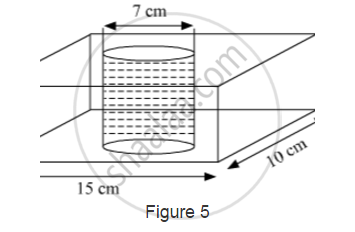
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid [take π=22/7]
If the radii of circular ends of a bucket 24cm high are 5cm and 15cm. find surface area of
bucket?
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4 \[\frac{2}{3}\] cm and height 3 cm. Find the number of cones so formed.
A rocket is in the form of a circular cylinder closed at the lower end and a cone of the same radius is attached to the top. The radius of the cylinder is 2.5 m, its height is 21 m and the slant height of the cone is 8 m. Calculate the total surface area of the rocket.
How many cubes of 10 cm edge can be put in a cubical box of 1 m edge?
The volume of a hemisphere is 19404 cm3. The total surface area of the hemisphere is
If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio ______.
