Advertisements
Advertisements
Question
From a cubical piece of wood of side 21 cm, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece. Find the surface area and volume of the remaining piece.
Advertisements
Solution
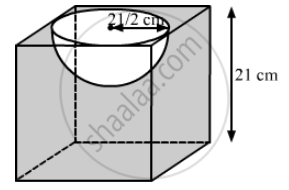
We have,
the edge of the cubical piece, a = 21 cm and
the radius of the hemisphere, `r = a/2=21/2`
The surface area of the remaining piece = TSA of cube + CSA of hemisphere -Area of
= 6a2 + 2πr2 - πr2
= 6a2 + πr2
`= 6 xx 21xx21xx22/7xx21/5xx21/2`
`= 21xx21(6 + 22/(7+4))`
`= 21xx21(6+11/14)`
`=21xx21((84+11)/14)`
`= 21xx3(95/2)`
= 2992.5 cm2
Also,
Volume of the remaining piece = volume of the cube - volume of the hemisphere
`= a^3 - 2/3pir^3`
`= 21xx21xx21 - 2/3xx22/7xx(21/2)xx(21/2)xx(21/2)`
`= 21xx21xx21xx(1-2/3xx22/7xx1/2xx1/2xx1/2)`
`= 21xx21xx21(1/1 - 11/42)`
`=21xx21xx21xx(42-11)/42`
`= 21xx21xx(31/2)`
= 6835.5 cm3
APPEARS IN
RELATED QUESTIONS
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m2.
(Note that the base of the tent will not be covered with canvas.) [Use `pi = 22/7`]
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimension 6cm \[\times\] 42cm \[\times\] 21 cm.
From a solid cube of side 7 cm , a conical cavity of height 7 cm and radius 3 cm is hollowed out . Find the volume of the remaining solid.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm, respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is 30 cm.
A hemispherical bowl of internal diameter 30 cm contains some liquid. This liquid is to be poured into cylindrical bottles of diameter 5 cm and height 6 cm each. Find the number of bottles required.
Water is flowing through a cylindrical pipe of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m per second. Determine the rise in level of water in the tank in half an hour.
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
If the areas of three adjacent faces of a cuboid are x, y and z, respectively, the volume of the cuboid is ______.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14)
The radius of spherical balloon increases from 8 cm to 12 cm. The ratio of the surface areas of balloon in two cases is ______.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
|
Khurja is a city in the Indian state of Uttar Pradesh famous for the pottery. Khurja pottery is traditional Indian pottery work which has attracted Indians as well as foreigners with a variety of tea sets, crockery and ceramic tile works. A huge portion of the ceramics used in the country is supplied by Khurja and is also referred as "The Ceramic Town". One of the private schools of Bulandshahr organised an Educational Tour for class 10 students to Khurja. Students were very excited about the trip. Following are the few pottery objects of Khurja.
Students found the shapes of the objects very interesting and they could easily relate them with mathematical shapes viz sphere, hemisphere, cylinder etc. |
Maths teacher who was accompanying the students asked the following questions:
- The internal radius of hemispherical bowl (filled completely with water) in I is 9 cm and the radius and height of the cylindrical jar in II are 1.5 cm and 4 cm respectively. If the hemispherical bowl is to be emptied in cylindrical jars, then how many cylindrical jars are required?
- If in the cylindrical jar full of water, a conical funnel of the same height and same diameter is immersed, then how much water will flow out of the jar?
A tent is in the shape of a cylinder surmounted by a conical top. If the height and radius of the cylindrical part are 3 m and 14 m respectively, and the total height of the tent is 13.5 m, find the area of the canvas required for making the tent, keeping a provision of 26 m2 of canvas for stitching and wastage. Also, find the cost of the canvas to be purchased at the rate of ₹ 500 per m2.
