Advertisements
Advertisements
Question
If the total surface area of a solid hemisphere is 462 cm2, then find its volume.
Solution
As , the total surface area of the solid hemisphere = 462 cm2
⇒ `3pir^2 = 462`
⇒ `3 xx 22/7 xx r^2 = 462`
⇒ `r^2 = (462 xx 7)/(3 xx 22)`
⇒ `r^2 = 49`
⇒ `r^2 = sqrt{49}`
⇒ r = 7 cm
Now, the volume of the solid hemisphere = `2/3 pir^3`
= `2/3 xx 22/7 xx 7 xx 7 xx 7`
= `2156/3` cm3
= `718 2/3 "cm"^3`
= 718.67 `"cm"^3`
APPEARS IN
RELATED QUESTIONS
The largest possible sphere is carved out of a wooden solid cube of side 7 em. Find the volume of the wood left. (Use\[\pi = \frac{22}{7}\]).
Prove that the surface area of a sphere is equal to the curved surface area of the circumference cylinder__?
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
The volume of a hemisphere is 2425 `1/2` cm3 . Find its curved surface area.
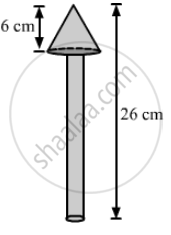
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
Five identical cubes, each of edge 5 cm, are placed adjacent to each other. Find the volume of the resulting cuboid.
Match the following columns:
| Column I | Column II |
| (a) The radii of the circular ends of a bucket, in the form of the frustum of a cone of height 30 cm, are 20 cm and 10 cm respectively. The capacity of the bucket is ........cm3. |
(p) 2418π |
| (b) The radii of the circular ends of a conical bucket of height 15 cm are 20 and 12 cm respectively. The slant height of the bucket is ........ cm. |
(q) 22000 |
| (c) The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. The total surface area of the bucket is .........cm2. |
(r) 12 |
| (d) Three solid metallic spheres of radii 3 cm, 4 cm and 5 cm are melted to form a single solid sphere. The diameter of the resulting sphere is ........ cm. |
(s) 17 |
A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere and hence find the surface area of this sphere.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
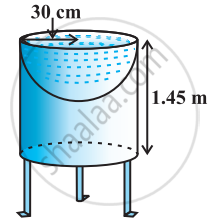
Ramesh made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.