Advertisements
Advertisements
Question
A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere and hence find the surface area of this sphere.
Solution
A cone has been reshaped in the sphere
Height of cone is 24 cm and the radius of the base is 6 cm
Volume of sphere = volume of cone
Volume of cone = `1/3`πr2h
Plugging the values in the formula we get
volume of cone = `1/3`π(6)224 = 288π cm3
Let the radius of sphere be r
Volume of sphere = `4/3`πr3
Since, the volume of cone = volume of sphere
Volume of sphere = 288π cm3
So,
288π = `4/3` πr3
⇒ 288 = `4/3`r3
⇒ r3 = 216
⇒ r = 6 cm
Hence, radius of reshaped sphere is 6 cm
Now, surface area of sphere = 4πr2
= 4π(6)2
= `144 × 22/7`
= 452.5 cm2
Therefore, surface area of sphere is 452.57 cm2
RELATED QUESTIONS
A toy is in the form of a cone of base radius 3.5 cm mounted on a hemisphere of base diameter 7 cm. If the total height of the toy is 15.5 cm, find the total surface area of the top (Use π = 22/7)
A toy is in the form of a cone surmounted on a hemisphere. The diameter of the base and the height of cone are 6cm and 4cm. determine surface area of toy?
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
A solid sphere of radius 'r' is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm, find the value of 'r'.
Find the volume of a solid in the form of a right circular cylinder with hemi-spherical ends whose total length is 2.7 m and the diameter of each hemi-spherical end is 0.7 m.
A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is
In a right circular cone, the cross-section made by a plane parallel to the base is a
A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of ₹ 50 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 10 per 100 cm2. (Take π = 3⋅14)
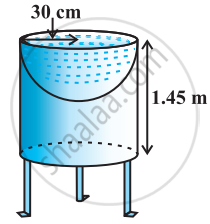
Ramesh made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.
The ratio of total surface area of a solid hemisphere to the square of its radius is ______.
