Advertisements
Advertisements
Question
Find the volume of a solid in the form of a right circular cylinder with hemi-spherical ends whose total length is 2.7 m and the diameter of each hemi-spherical end is 0.7 m.
Solution
Radius of hemispherical ends = radius of cylinder
`=1/2 xx 0.7`
`=7/20 m`

Total length = 2.7 m.
Height of cylinder
`=2.7 - 2 xx 7/20`
`= 2m`
Volume of two hemispheres
`=2 (2/3 pir^3)`
`=4/3 pir^3`
`=4/3 xx 22/7 xx (7/20)^3`
`=4/3 xx 22 /7 xx (343)/(800)`
` = 0.1797 m^3`
Volume of cylinders
` =pir^2h`
`=22/7 xx (7/20)^2 xx 2`
`=0.77 m^2`
Hence,
Volume of solid = 0.1797+0.77 = 0.95 m3
APPEARS IN
RELATED QUESTIONS
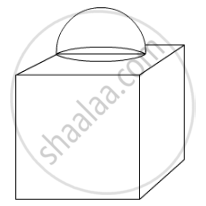
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m2.
(Note that the base of the tent will not be covered with canvas.) [Use `pi = 22/7`]
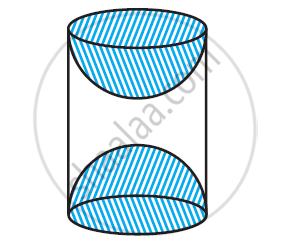
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
A frustum of a right circular cone has a diameter of base 20 cm, of top 12 cm, and height 3 cm. Find the area of its whole surface and volume.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4 \[\frac{2}{3}\] cm and height 3 cm. Find the number of cones so formed.
A rocket is in the form of a circular cylinder closed at the lower end and a cone of the same radius is attached to the top. The radius of the cylinder is 2.5 m, its height is 21 m and the slant height of the cone is 8 m. Calculate the total surface area of the rocket.
A solid metallic sphere of diameter 21 cm is melted and recast into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio ______.
