Question

A farmer connects a pipe of internal diameter 20 cm form a canal into a cylindrical tank in his field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?

Answer 1

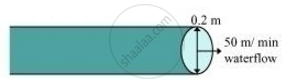
Consider an area of cross-section of the pipe as shown in the figure.

Radius (r₁) of circular end of pipe = `20/200` = 0.1 m

Area of cross-section = `pixxr_1^2 = pixx(0.1)^2 = 0.01pi m^2`

Speed of water = 3 km/h = `3000/60` = 50 meter/min

Volume of water that flows in 1 minute from pipe = 50 × 0.01 π = 0.5π m³

Volume of water that flows in t minutes from pipe = t × 0.5π m³

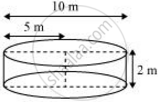
Radius (r₂) of circular end of cylindrical tank = `10/2` = 5m

Depth (h₂) of cylindrical tank = 2 m

Let the tank be filled completely in t minutes.

Volume of water filled in tank in t minutes is equal to the volume of water flowed in t minutes from the pipe.

Volume of water that flows in t minutes from pipe = Volume of water in tank

t × 0.5π = π ×(r₂)² × h₂

t × 0.5 = 5² ×2

t = 100

Therefore, the cylindrical tank will be filled in 100 minutes.