Advertisements
Advertisements
Question
Water in canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. how much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Solution
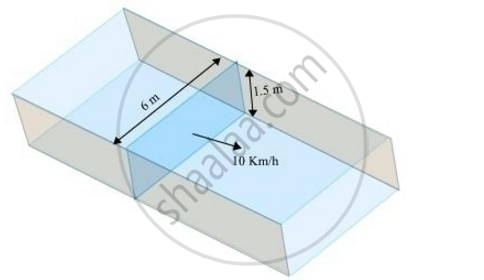
Consider an area of cross-section of canal as ABCD.
Area of cross-section = 6 × 1.5 = 9 m2
Speed of water = 10 km/h = 10000/60 metre/min
Volume of water that flows in 1 minute from canal = 9 x 10000/60 =1500 m3
Volume of water that flows in 30 minutes from canal = 30 × 1500 = 45000 m3
Let the irrigated area be A. Volume of water irrigating the required area will be equal to the volume of water that flowed in 30 minutes from the canal.
Vol. of water flowing in 30 minutes from canal = Vol. of water irrigating the reqd. area
4500 = (Ax8)/100
A = 562500 m2
Therefore, area irrigated in 30 minutes is 562500 m2.
RELATED QUESTIONS
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm? [Use π=22/7]
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm. Find the radius and slant height of the heap.
Three cubes of a metal whose edges are in the ratios 3 : 4 : 5 are melted and converted into a single cube whose diagonal is \[12\sqrt{3}\]. Find the edges of the three cubes.
A right circular cylinder of radius r and height h (h = 2r) just encloses a sphere of diameter
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively are melted to form a single solid sphere. Find the radius of the resulting sphere.
The internal and external diameters of a hollow hemispherical shell are 6 cm and 10 cm, respectively. It is melted and recast into a solid cone of base diameter 14 cm. Find the height of the cone so formed.
A solid cylinder of radius r and height h is placed over other cylinder of same height and radius. The total surface area of the shape so formed is 4πrh + 4πr2.
A solid metallic hemisphere of radius 8 cm is melted and recasted into a right circular cone of base radius 6 cm. Determine the height of the cone.
A solid piece of metal in the form of a cuboid of dimensions 11 cm × 7 cm × 7 cm is melted to form 'n' number of solid spheres of radii `7/2` cm each. Find the value of n.
The volume of a right circular cone whose area of the base is 156 cm2 and the vertical height is 8 cm, is ______.
