Advertisements
Advertisements
Question
A right circular cylinder of radius r and height h (h = 2r) just encloses a sphere of diameter
Options
h
r
2r
2h
Solution
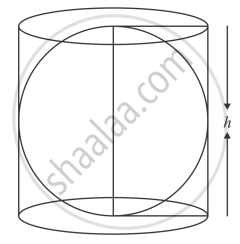
Radius of cylinder = r
Height = h
= 2r
Since, the sphere fitted the cylinder.
i.e., diameter of sphere = height of cylinder.
`d = h = 2r`
`d = 2r`
APPEARS IN
RELATED QUESTIONS
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm. Find the radius and slant height of the heap.
Water in canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. how much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
A well of diameter 3 m is dug 14 m deep. The soil taken out of it is spread evenly all around it to a width of 5 m to form an embankment. Find the height of the embankment ?
If four times the sum of the areas of two circular faces of a cylinder of height 8 cm is equal to twice the curve surface area, then diameter of the cylinder is
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively are melted to form a single solid sphere. Find the radius of the resulting sphere.
During conversion of a solid from one shape to another, the volume of the new shape will ______.
A cylindrical bucket, 32 cm high and 18 cm of radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
A solid metallic hemisphere of radius 8 cm is melted and recasted into a right circular cone of base radius 6 cm. Determine the height of the cone.
