Advertisements
Advertisements
Question
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm? [Use π=22/7]
Solution
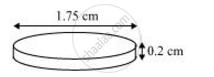
Coins are cylindrical in shape.
Height (h1) of cylindrical coins = 2 mm = 0.2 cm
Radius (r) of circular end of coins = 1.75/2 =0.875 cm
Let n coins be melted to form the required cuboids.
Volume of n coins = Volume of cuboids
nxπxr2xh1 = lxbxh
n x π x (0.875)2 x 0.2 = 5.5 x 10 x 3.5
`n = (5.5xx10xx3.5xx7)/((0.875)^2xx0.2xx22) = 400`
Therefore, the number of coins melted to form such a cuboid is 400.
APPEARS IN
RELATED QUESTIONS
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm .
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape formed.
A right circular cylinder of radius r and height h (h = 2r) just encloses a sphere of diameter
The radii of the ends of a bucket 16 cm height are 20 cm and 8 cm. The curved surface area of the bucket is
The diameters of the top and the bottom portions of a bucket are 42 cm and 28 cm respectively. If the height of the bucket is 24 cm, then the cost of painting its outer surface at the rate of 50 paise / cm2 is
A solid metallic hemisphere of radius 8 cm is melted and recasted into a right circular cone of base radius 6 cm. Determine the height of the cone.
|
A company deals in casting and moulding of metal on orders received from its clients. In one such order, company is supposed to make 50 toys in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of hemisphere. If the radius of the base of the cone is 21 cm and height is 28 cm.
|
- find the volume of 50 toys:
- fine the ratio of the volume of hemisphere to the volume of cone.
The volume of a right circular cone whose area of the base is 156 cm2 and the vertical height is 8 cm, is ______.