Advertisements
Advertisements
प्रश्न
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm? [Use π=22/7]
उत्तर
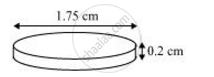
Coins are cylindrical in shape.
Height (h1) of cylindrical coins = 2 mm = 0.2 cm
Radius (r) of circular end of coins = 1.75/2 =0.875 cm
Let n coins be melted to form the required cuboids.
Volume of n coins = Volume of cuboids
nxπxr2xh1 = lxbxh
n x π x (0.875)2 x 0.2 = 5.5 x 10 x 3.5
`n = (5.5xx10xx3.5xx7)/((0.875)^2xx0.2xx22) = 400`
Therefore, the number of coins melted to form such a cuboid is 400.
APPEARS IN
संबंधित प्रश्न
A solid frustum is of height 8 cm. If the radii of its lower and upper ends are 3 cm and 9 cm respectively, then its slant height is
If two solid-hemisphere s of same base radius r are joined together along their bases , then curved surface area of this new solid is
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively are melted to form a single solid sphere. Find the radius of the resulting sphere.
During conversion of a solid from one shape to another, the volume of the new shape will ______.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied out on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
A solid cylinder of radius r and height h is placed over other cylinder of same height and radius. The total surface area of the shape so formed is ______.
During conversion of a solid from one shape to another, the volume of the new shape will ______.
A solid metallic hemisphere of radius 8 cm is melted and recasted into a right circular cone of base radius 6 cm. Determine the height of the cone.
A solid piece of metal in the form of a cuboid of dimensions 11 cm × 7 cm × 7 cm is melted to form 'n' number of solid spheres of radii `7/2` cm each. Find the value of n.
|
A company deals in casting and moulding of metal on orders received from its clients. In one such order, company is supposed to make 50 toys in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of hemisphere. If the radius of the base of the cone is 21 cm and height is 28 cm.
|
- find the volume of 50 toys:
- fine the ratio of the volume of hemisphere to the volume of cone.