Advertisements
Advertisements
प्रश्न
A farmer connects a pipe of internal diameter 20 cm form a canal into a cylindrical tank in his field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
उत्तर
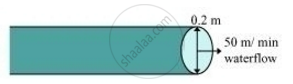
Consider an area of cross-section of the pipe as shown in the figure.
Radius (r1) of circular end of pipe = `20/200` = 0.1 m
Area of cross-section = `pixxr_1^2 = pixx(0.1)^2 = 0.01pi m^2`
Speed of water = 3 km/h = `3000/60` = 50 meter/min
Volume of water that flows in 1 minute from pipe = 50 × 0.01 π = 0.5π m3
Volume of water that flows in t minutes from pipe = t × 0.5π m3
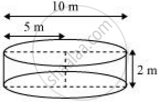
Radius (r2) of circular end of cylindrical tank = `10/2` = 5m
Depth (h2) of cylindrical tank = 2 m
Let the tank be filled completely in t minutes.
Volume of water filled in tank in t minutes is equal to the volume of water flowed in t minutes from the pipe.
Volume of water that flows in t minutes from pipe = Volume of water in tank
t × 0.5π = π ×(r2)2 × h2
t × 0.5 = 52 ×2
t = 100
Therefore, the cylindrical tank will be filled in 100 minutes.
संबंधित प्रश्न
Metallic spheres of radii 6 cm, 8 cm, and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform. [Use Π = 22/7]
Water in canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. how much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into toys with the shape of a right circular cone mounted on a hemisphere of radius 3 cm.If the height of the toy is 12 cm, find the number of toys so formed.
A solid frustum is of height 8 cm. If the radii of its lower and upper ends are 3 cm and 9 cm respectively, then its slant height is
If four times the sum of the areas of two circular faces of a cylinder of height 8 cm is equal to twice the curve surface area, then diameter of the cylinder is
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied out on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
During conversion of a solid from one shape to another, the volume of the new shape will ______.
A solid cylinder of radius r and height h is placed over other cylinder of same height and radius. The total surface area of the shape so formed is 4πrh + 4πr2.
A solid piece of metal in the form of a cuboid of dimensions 11 cm × 7 cm × 7 cm is melted to form 'n' number of solid spheres of radii `7/2` cm each. Find the value of n.
