Advertisements
Advertisements
प्रश्न
A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere and hence find the surface area of this sphere.
उत्तर
A cone has been reshaped in the sphere
Height of cone is 24 cm and the radius of the base is 6 cm
Volume of sphere = volume of cone
Volume of cone = `1/3`πr2h
Plugging the values in the formula we get
volume of cone = `1/3`π(6)224 = 288π cm3
Let the radius of sphere be r
Volume of sphere = `4/3`πr3
Since, the volume of cone = volume of sphere
Volume of sphere = 288π cm3
So,
288π = `4/3` πr3
⇒ 288 = `4/3`r3
⇒ r3 = 216
⇒ r = 6 cm
Hence, radius of reshaped sphere is 6 cm
Now, surface area of sphere = 4πr2
= 4π(6)2
= `144 × 22/7`
= 452.5 cm2
Therefore, surface area of sphere is 452.57 cm2
संबंधित प्रश्न
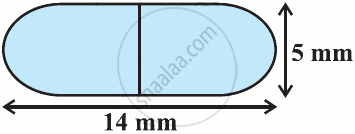
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
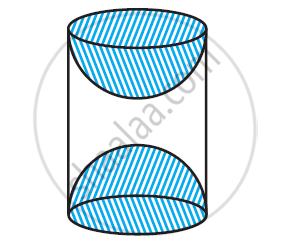
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
Water in a canal, 5·4 m wide and 1·8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
A cylindrical tub, whose diameter is 12 cm and height 15 cm is full of ice-cream. The whole ice-cream is to be divided into 10 children in equal ice-cream cones, with conical base surmounted by hemispherical top. If the height of conical portion is twice the diameter of base, find the diameter of conical part of ice-cream cone ?
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
A solid metallic sphere of diameter 21 cm is melted and recast into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.
If the areas of three adjacent faces of a cuboid are x, y and z, respectively, the volume of the cuboid is ______.
The shape of a gilli, in the gilli-danda game (see figure), is a combination of ______.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
