Advertisements
Advertisements
प्रश्न
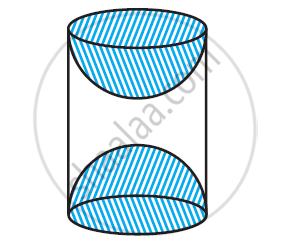
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
उत्तर
Given that,
Radius (r) of cylindrical part = Radius (r) of hemispherical part = 3.5 cm
Height of cylindrical part (h) = 10 cm
Surface area of article = CSA of cylindrical part + 2 × CSA of hemispherical part
= 2πrh + 2 × 2πr2
= 2π × 3.5 × 10 + 2 × 2π × 3.5 × 3.5
= 70π + 49π
= 119π
= 17 × 22
= 374 cm2
APPEARS IN
संबंधित प्रश्न
Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs Rs. 100 per sq. m, find the amount, the associations will have to pay. What values are shown by these associations? [Use π=22/7]
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area.
[Use π=22/7]
In Fig. 4, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use `pi=22/7` and `sqrt5=2.236`)

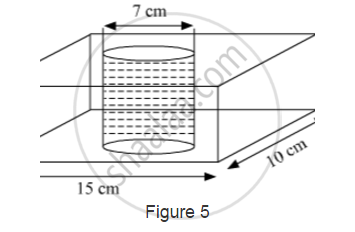
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m2.
(Note that the base of the tent will not be covered with canvas.) [Use `pi = 22/7`]
A frustum of a right circular cone has a diameter of base 20 cm, of top 12 cm, and height 3 cm. Find the area of its whole surface and volume.
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
A cylindrical tub, whose diameter is 12 cm and height 15 cm is full of ice-cream. The whole ice-cream is to be divided into 10 children in equal ice-cream cones, with conical base surmounted by hemispherical top. If the height of conical portion is twice the diameter of base, find the diameter of conical part of ice-cream cone ?
Find the number of metallic circular discs with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm .
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
Three solid spheres of radii 3, 4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
The volume of a hemisphere is 2425 `1/2` cm3 . Find its curved surface area.
A hemispherical bowl of internal diameter 30 cm contains some liquid. This liquid is to be poured into cylindrical bottles of diameter 5 cm and height 6 cm each. Find the number of bottles required.
A copper wire of diameter 6 mm is evenly wrapped on a cylinder of length 18 cm and diameter 49 cm to cover its whole surface. Find the length and the volume of the wire. If the density of the copper be 8.8 g per cm3, then find the weight of the wire.
Five identical cubes, each of edge 5 cm, are placed adjacent to each other. Find the volume of the resulting cuboid.
If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio ______.
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
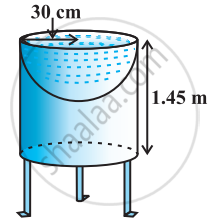
Ramesh made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath.
Statement A (Assertion): Total Surface area of the top is the sum of the curved surface area of the hemisphere and the curved surface area of the cone.
Statement R( Reason): Top is obtained by joining the plane surfaces of the hemisphere and cone together.

