Advertisements
Advertisements
Question
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
Solution
The height of the frustum cone is h= 8 m. The radii of the end circles of the frustum are r1 = 13m and r2 =7m.
The slant height of the frustum cone is
`l=sqrt((r_1-r_2)^2+h^2`
`=sqrt((13-7)^2+8^2`
`=sqrt(100)`
= 10 meter
The curved surface area of the frustum is
`S_1=pi(r_1+r_2)xxl`
= π x (13+7) x 10
= π 20 x 10
= 200π m2
The base-radius of the upper cap cone is 7m and the slant height is 12m. Therefore, the curved surface area of the upper cap cone is
S2 = π x 7 x 12
`=22/7xx7xx12`
= 22 x 12
= 264 m2
Hence, the total canvas required for the tent is
S1 + S2 = 200π + 264
= 892.57 m2
Hence total canvas is 892.57 m2
APPEARS IN
RELATED QUESTIONS
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. [Use `pi = 22/7`]
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
A tent of height 77dm is in the form a right circular cylinder of diameter 36m and height 44dm surmounted by a right circular cone. Find the cost of canvas at Rs.3.50 per m2 ?
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
Two solid cones A and B are placed in a cylindrical tube as shown in fig .16.76. The ratio of their capacities are 2: 1 . Find the heights and capacities of the cones . Also, find the volume of the remaining portion of the cylinder.
If the total surface area of a solid hemisphere is 462 cm2, then find its volume.
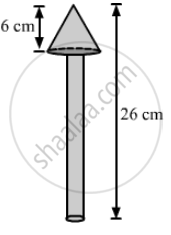
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
If two solid hemispheres of the same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
The boilers are used in thermal power plants to store water and then used to produce steam. One such boiler consists of a cylindrical part in middle and two hemispherical parts at its both ends.
Length of the cylindrical part is 7 m and radius of cylindrical part is `7/2` m.
Find the total surface area and the volume of the boiler. Also, find the ratio of the volume of cylindrical part to the volume of one hemispherical part.

