Advertisements
Advertisements
Question
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. [Use `pi = 22/7`]
Solution
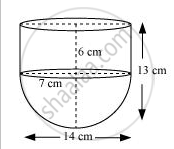
It can be observed that radius (r) of the cylindrical part and the hemispherical part is the same (i.e., 7 cm).
Height of hemispherical part = Radius = 7 cm
Height of cylindrical part (h) = 13 − 7 = 6 cm
Inner surface area of the vessel = CSA of cylindrical part + CSA of hemispherical part
= 2πrh + 2πr2
Inner surface are of vessel = `2 xx 22/7 xx 7 xx 6+2 xx 22/7 xx 7 xx 7`
= 44 (6 + 7)
`= 44xx13`
= 572 cm2
APPEARS IN
RELATED QUESTIONS
Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs Rs. 100 per sq. m, find the amount, the associations will have to pay. What values are shown by these associations? [Use π=22/7]
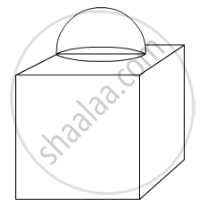
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy [Use π =`22/7`]
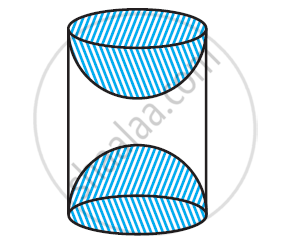
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
[Use `pi = 22/7`]
Water in a canal, 5·4 m wide and 1·8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
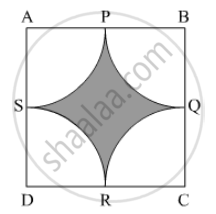
Find the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]
A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10 cm. and 6 cm, respectively. Find the total surface area of the solid. (Use π =`22/7`)
A vessel is in the form of hemispherical bowl surmounted by a hollow cylinder of same diameter. The diameter of the hemispherical bowl is 14 cm and the total height of the vessel is 13 cm. Find the total surface area of the vessel. `[\text{Use}pi=22/7]`
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimension 6cm \[\times\] 42cm \[\times\] 21 cm.
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4 \[\frac{2}{3}\] cm and height 3 cm. Find the number of cones so formed.
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is 108 cm and the diameter of the cylinder is 36 cm, find the cost of polishing the surface at the rate of 7 paise per cm2 .
If the total surface area of a solid hemisphere is 462 cm2, then find its volume.
In a village, a well with 10 m inside diameter, is dug 14 m deep. Earth taken out of it is spread all around to a width 5 m to form an embankment. Find the height of the embankment. What value of the villagers is reflected here?
Match the following columns:
| Column I | Column II |
| (a) The radii of the circular ends of a bucket, in the form of the frustum of a cone of height 30 cm, are 20 cm and 10 cm respectively. The capacity of the bucket is ........cm3. |
(p) 2418π |
| (b) The radii of the circular ends of a conical bucket of height 15 cm are 20 and 12 cm respectively. The slant height of the bucket is ........ cm. |
(q) 22000 |
| (c) The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. The total surface area of the bucket is .........cm2. |
(r) 12 |
| (d) Three solid metallic spheres of radii 3 cm, 4 cm and 5 cm are melted to form a single solid sphere. The diameter of the resulting sphere is ........ cm. |
(s) 17 |
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is 6πr2.
Statement A (Assertion): Total Surface area of the top is the sum of the curved surface area of the hemisphere and the curved surface area of the cone.
Statement R( Reason): Top is obtained by joining the plane surfaces of the hemisphere and cone together.

