Advertisements
Advertisements
Question
Water in a canal, 5·4 m wide and 1·8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
Solution
Width of the canal = 5.4 m
Depth of the canal = 1.8 m
Height of the standing water needed for irrigation = 10 cm = 0.1 m
Speed of the flowing water = 25 km/h = `25000/60=1250/3` m/min
Volume of water flowing out of the canal in 1 min
= Area of opening of canal x `1250/3`
`= 5.4 xx 1.8 xx 1250/3`
=4050 m3
∴ Volume of water flowing out of the canal in 40 min = 40 × 4050 m3 = 162000 m3
Now,
Area of irrigation = `"Volume of water flowing out from canal in 40 min"/"Height of the standing water needed for irrigation"`
`= 162000/0.1`
`= 1620000 m^2`
= 162 hectare (∵ 1 hectare = 10000 m2)
Thus, the area irrigated in 40 minutes is 162 hectare.
APPEARS IN
RELATED QUESTIONS
Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs Rs. 100 per sq. m, find the amount, the associations will have to pay. What values are shown by these associations? [Use π=22/7]
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy [Use π =`22/7`]
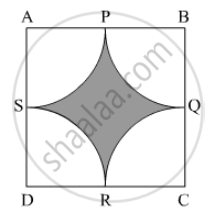
Find the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]
The internal and external diameters of a hollow hemisphere vessel are 21cm and 25.2 cm The cost of painting 1cm2 of the surface is 10paise. Find total cost to paint the vessel all
over______?
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively.The radii of the hemispherical and conical parts are the same as that of the cylindrical part.Find the surface area of the toy if the total height of the toy is 30 cm.
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9 `cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
A solid sphere of radius 'r' is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm, find the value of 'r'.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of ₹5 per 100 sq cm. [Use ππ = 3.14]
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single large cube. Find the edge of the new cube formed.
Statement A (Assertion): Total Surface area of the top is the sum of the curved surface area of the hemisphere and the curved surface area of the cone.
Statement R( Reason): Top is obtained by joining the plane surfaces of the hemisphere and cone together.

