Advertisements
Advertisements
Questions
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy [Use π =`22/7`]
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius on its circular face. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution
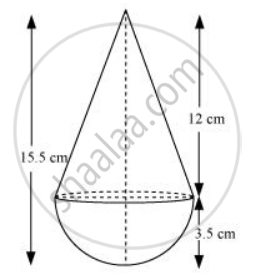
Radius of hemisphere = 3.5 cm
total height of the toy = 15.5 cm.
Surface area of cone `=pirl`
`l = sqrt((12)^2 + (3.5)^2)`
`= sqrt156.25`
`=12.5 cm`
Therefore,
Surface area of cone
`= 22/7 xx 3.5 xx 12.5`
`=137.5 cm^2`
Surface area of hemisphere `=2pir^2`
`= 2 xx 22/7 xx 3.5 xx 3.5`
`= 77 cm^2`
Therefore,
Total surface area of the toy
`=137.5 + 77`
`=214.5 cm^2`
Volume of cone
`=1/3pir^2h`
`=1/3 xx 22/7 xx (3.51^2 xx 12)`
`=154 cm^2`
Volume of hemisphere
`=2/3pir^3`
`= 2/3 xx 22/7 xx (3.5)^3`
`= 89.83 cm `
Therefore,
Total volume of the toy
`= (154 + 89.83) cm^3`
`= 243.83 cm^3`
APPEARS IN
RELATED QUESTIONS
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/h. How much area will it irrigate in 10 minutes, if 8 cm of standing water is needed for irrigation?
A solid wooden toy is in the form of a hemisphere surrounded by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 `5/6` cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs 10 per cm2 .[Use`pi=22/7`]
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid [take π=22/7]
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9 `cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
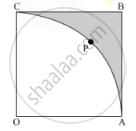
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimension 6cm \[\times\] 42cm \[\times\] 21 cm.
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is \[\left( r_1^3 + r_2^3 \right)^\frac{1}{3}\].
Two solid cones A and B are placed in a cylindrical tube as shown in fig .16.76. The ratio of their capacities are 2: 1 . Find the heights and capacities of the cones . Also, find the volume of the remaining portion of the cylinder.
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
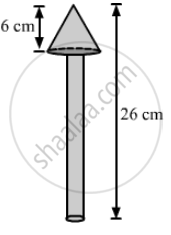
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
A solid metallic sphere of diameter 21 cm is melted and recast into a number of smaller cones, each of diameter 3.5 cm and height 3 cm. Find the number of cones so formed.
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single large cube. Find the edge of the new cube formed.
The curved surface area of glass having radii 3 cm and 4 cm respectively and slant height 10 cm is ______.
The total surface area of a solid hemisphere of radius 7 cm is ______.
|
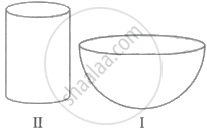
Khurja is a city in the Indian state of Uttar Pradesh famous for the pottery. Khurja pottery is traditional Indian pottery work which has attracted Indians as well as foreigners with a variety of tea sets, crockery and ceramic tile works. A huge portion of the ceramics used in the country is supplied by Khurja and is also referred as "The Ceramic Town". One of the private schools of Bulandshahr organised an Educational Tour for class 10 students to Khurja. Students were very excited about the trip. Following are the few pottery objects of Khurja.
Students found the shapes of the objects very interesting and they could easily relate them with mathematical shapes viz sphere, hemisphere, cylinder etc. |
Maths teacher who was accompanying the students asked the following questions:
- The internal radius of hemispherical bowl (filled completely with water) in I is 9 cm and the radius and height of the cylindrical jar in II are 1.5 cm and 4 cm respectively. If the hemispherical bowl is to be emptied in cylindrical jars, then how many cylindrical jars are required?
- If in the cylindrical jar full of water, a conical funnel of the same height and same diameter is immersed, then how much water will flow out of the jar?