Advertisements
Advertisements
Question
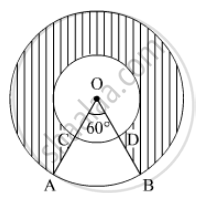
In Figure , two concentric circles with centre O, have radii 21cm and 42 cm. If ∠ AOB = 60°, find the area of the shaded region. [use π=22/7]
Solution 1
Solution:
Given :
Radii of inner circle = 21 cm = r
Radii of outer circle = 42 cm = R
∠AOB = θ = 60°
Also,
Area of ring = π(R2-r2)
Area of a sector `= theta/360 pir^2`
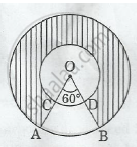
The area of shaded region = Area of ring – Area of ABCD
= Area of ring – Area of sector of Outer Circle - Area of sector of Inner Circle
`=pi(R^2-r^2)-(pi(R^2-r^2))/1 xx theta/360`
`=pi(R^2-r^2)[1-theta/360]`
`=22/7(42^2-21^2)(1-60/360)`
`=3465 cm^2`
Solution 2
Solution:
Given :
Radii of inner circle = 21 cm = r
Radii of outer circle = 42 cm = R
∠AOB = θ = 60°
Also,
Area of ring = π(R2-r2)
Area of a sector `= theta/360 pir^2`

The area of shaded region = Area of ring – Area of ABCD
= Area of ring – Area of sector of Outer Circle - Area of sector of Inner Circle
`=pi(R^2-r^2)-(pi(R^2-r^2))/1 xx theta/360`
`=pi(R^2-r^2)[1-theta/360]`
`=22/7(42^2-21^2)(1-60/360)`
`=3465 cm^2`
Solution 3
Given: Radius of the inner circle with radius OC, r = 21 cm
Radius of the inner circle with radius OA, R = 42 cm
∠AOB = 60°
Area of the circular ring
`= piR^2 - pir^2`
`=pi[R^2 - r^2]`
`=pi[42^2 - 21^2] cm^2`
Area of ACDB = area of sector AOB − area of COD
`= 60/360 xx pi xx R^2 - 60/300 xx pi xx r^2`
`= 60/360 xx pi[R^2 - r^2]`
`= 60/360 xx pi[42^2 - 21^2]`
Area of shaded region = area of circular ring − area of ACDB
`= pi[42^2 - 21^2] - 60/360 pi [42^2 - 21^2]`
`= pi[42^2 - 21^2][1 - 60/360]`
`= 22/7 (42 - 21) (42 + 21) xx 300/360`
`=3465 cm^2`
APPEARS IN
RELATED QUESTIONS
Find the area of the rhombus, the length of whose diagonals are 30 cm and 16 cm. Also, find the perimeter of the rhombus.
The radius of a sector of a circle is 7 cm. If the measure of the arc of the sector is 210°, find the area of the sector in case.
In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. [π = 3.14]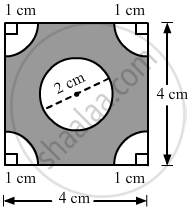
The perimeter of a circular field is 242 m. The area of the field is
The diameter of a wheel is 84 cm. How many revolutions will it make to cover 792 m?
A conical tent requires 264 m2 of canvas. If the slant height is 12 m, find the vertical height of the cone.
Find the area and perimeter of the following semi-circle :
Diameter= 5.6 cm
Find the area and perimeter of the following semicircles: Radius = 1.4cm
Find the area and perimeter of the following semicircles: Diameter = 7cm
Circumference of a circle of diameter 5 cm is ______.
