Advertisements
Advertisements
Question
Find the ratio in which the line segment joining the points A(3,- 3) and B(- 2, 7) is divided by x-axis. Also find the coordinates of the point of division.
Solution
Solution:
Point p lies on x axis so it’s ordinate is 0 (Using section formula)
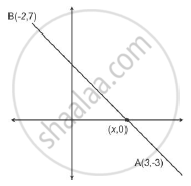
Let the ratio be k: 1 Let the coordinate of the point be P(x , 0) As given A(3,-3) and B(-2,7)
The co-ordinates of the point P(x,y), which divide the line segment joining the points A(x1,y1) and B(x2,y2), internally in the ratio m1:m2 are
`P_x=(mx_2+nx_1)/(m+n)`
`P_y=(my_2+ny_1)/(m+n)`
Hence, A(3,-3) be the co-ordinates (x1,y1) and B(-2,7) be the co-ordinates (x2,y2)
m = k
n = 1
0 = k x 7 + 1 x -3 / (k+1)
0(k+1) =7k -3
0 =7k - 3
3=7k
k = 3 /7
k:1 = 3 : 7
`P_x=(mx_2+nx_1)/(m+n)`
`P_x=[(3/7xx-2)+(1xx3)]/(3/7+1)=2.41`
APPEARS IN
RELATED QUESTIONS
Construct the circumcircle and incircle of an equilateral triangle ABC with side 6 cm and centre O. Find the ratio of radii of circumcircle and incircle.
Construct a triangle ABC in which BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are`3/4` times the corresponding sides of ΔABC.
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are`4/5` times the corresponding sides of ΔABC.
Construct a triangle similar to a given ΔABC such that each of its sides is (5/7)th of the corresponding sides of Δ ABC. It is given that AB = 5 cm, BC = 7 cm and ∠ABC = 50°.
Construct a ΔABC in which AB = 5 cm. ∠B = 60° altitude CD = 3cm. Construct a ΔAQR similar to ΔABC such that side ΔAQR is 1.5 times that of the corresponding sides of ΔACB.
∆AMT ~ ∆AHE. In ∆AMT, AM = 6.3 cm, ∠TAM = 50°, AT = 5.6 cm. `"AM"/"AH" = 7/5`. Construct ∆AHE.
Find the ratio in which point P(k, 7) divides the segment joining A(8, 9) and B(1, 2). Also find k.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are \[\frac{3}{5}\] times the corresponding sides of the given triangle.
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm, ∠D = 30°, ∠N = 20° and `"HP"/"ED" = 4/5`. Then construct ΔRHP and ΔNED
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

