Advertisements
Advertisements
प्रश्न
Find the ratio in which the line segment joining the points A(3,- 3) and B(- 2, 7) is divided by x-axis. Also find the coordinates of the point of division.
उत्तर
Solution:
Point p lies on x axis so it’s ordinate is 0 (Using section formula)
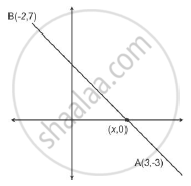
Let the ratio be k: 1 Let the coordinate of the point be P(x , 0) As given A(3,-3) and B(-2,7)
The co-ordinates of the point P(x,y), which divide the line segment joining the points A(x1,y1) and B(x2,y2), internally in the ratio m1:m2 are
`P_x=(mx_2+nx_1)/(m+n)`
`P_y=(my_2+ny_1)/(m+n)`
Hence, A(3,-3) be the co-ordinates (x1,y1) and B(-2,7) be the co-ordinates (x2,y2)
m = k
n = 1
0 = k x 7 + 1 x -3 / (k+1)
0(k+1) =7k -3
0 =7k - 3
3=7k
k = 3 /7
k:1 = 3 : 7
`P_x=(mx_2+nx_1)/(m+n)`
`P_x=[(3/7xx-2)+(1xx3)]/(3/7+1)=2.41`
APPEARS IN
संबंधित प्रश्न
Determine a point which divides a line segment of length 12 cm internally in the ratio 2 : 3 Also, justify your construction.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are 5/3th times the corresponding sides of the given triangle.
Find the ratio in which point P(k, 7) divides the segment joining A(8, 9) and B(1, 2). Also find k.
Choose the correct alternative:
∆ABC ∼ ∆AQR. `"AB"/"AQ" = 7/5`, then which of the following option is true?
ΔABC ~ ΔPBR, BC = 8 cm, AC = 10 cm , ∠B = 90°, `"BC"/"BR" = 5/4` then construct ∆ABC and ΔPBR
To construct a triangle similar to a given ΔABC with its sides `3/7` of the corresponding sides of ΔABC, first draw a ray BX such that ∠CBX is an acute angle and X lies on the opposite side of A with respect to BC. Then locate points B1, B2, B3, ... on BX at equal distances and next step is to join ______.
If the perpendicular distance between AP is given, which vertices of the similar triangle would you find first?
Match the following based on the construction of similar triangles, if scale factor `(m/n)` is.
| Column I | Column II | ||
| i | >1 | a) | The similar triangle is smaller than the original triangle. |
| ii | <1 | b) | The two triangles are congruent triangles. |
| iii | =1 | c) | The similar triangle is larger than the original triangle. |
Construction of similar polygons is similar to that of construction of similar triangles. If you are asked to construct a parallelogram similar to a given parallelogram with a given scale factor, which of the given steps will help you construct a similar parallelogram?
By geometrical construction, it is possible to divide a line segment in the ratio `sqrt(3) : 1/sqrt(3)`.
