Advertisements
Advertisements
प्रश्न
Determine a point which divides a line segment of length 12 cm internally in the ratio 2 : 3 Also, justify your construction.
उत्तर
Given that
Determine a point which divides a line segment of length 12cminternally in the ratio of 2:3.
We follow the following steps to construct the given
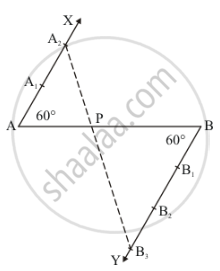
Step of construction
Step: I- First of all we draw a line segment AB = 12 cm.
Step: II- We draw a ray AX making an acute angle ∠BAX = 60° with AB.
Step: III- Draw a ray BY parallel to AX by making an acute angle ∠ABY = ∠BAX.
Step IV- Mark of two points A1, A2 on AX and three points B1, B2, B3 on BY in such a way that AA1 = A1A2 = BB1 = B1B2 = B2B3.
Step: V- Joins A2B3 and this line intersects AB at a point P.
Thus, P is the point dividing AB internally in the ratio of 2:3
Justification:
In ΔAA2P and ΔBB3P we have
∠A2AP = ∠PBB3 [∠ABY = ∠BAX]
And ∠APA2 = ∠BPB3 [Vertically opposite angle]
So, AA similarity criterion, we have
ΔAA2P ≈ ΔBB3P
`(A A_2)/(BB_3)=(AP)/(BP)`
`(AP)/(BP)=2/3`
APPEARS IN
संबंधित प्रश्न
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are`4/5` times the corresponding sides of ΔABC.
Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to (3/4)th of the corresponding sides of ΔABC.
Construct the circumcircle and incircle of an equilateral ∆XYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
Given A(4, –3), B(8, 5). Find the coordinates of the point that divides segment AB in the ratio 3 : 1.
ΔABC ~ ΔPBR, BC = 8 cm, AC = 10 cm , ∠B = 90°, `"BC"/"BR" = 5/4` then construct ∆ABC and ΔPBR
To divide a line segment AB in the ratio 4 : 7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1, A2, A3, .... are located at equal distances on the ray AX and the point B is joined to ______.
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

The point W divides the line XY in the ratio m : n. Then, the ratio of lengths of the line segments XY : WX is ______.
To divide a line segment, the ratio of division must be ______.
Draw a line segment of length 7.5 cm and divide it in the ratio 1:3.
