Advertisements
Advertisements
प्रश्न
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
उत्तर
Given that
Determine a point which divides a line segment of length 9 cm internally in the ratio of 4:3.
We follow the following steps to construct the given
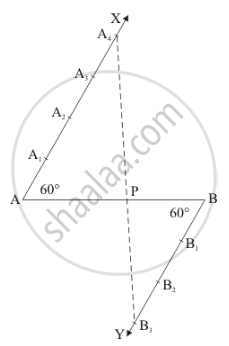
Step of construction
Step: I- First of all we draw a line segment AB = 9cm.
Step: II- We draw a ray AX making an acute angle ∠BAX = 60° with AB.
Step: III- Draw a ray BY parallel to AX by making an acute angle ∠ABY = ∠BAX.
Step IV- Mark of two points A1, A2, A3, A4 on AX and three points B1, B2, B3 on BY in such a way that AA1 = A1A2 = A2A3 = A3A4 = BB1 = B1B2 = B2B3.
Step: V- Joins A4B3 and this line intersects AB at a point P.
Thus, P is the point dividing AB internally in the ratio of 4:3
Justification:
In ΔAA4P and ΔBB3P we have
∠A4AP = ∠PBB3 [∠ABY = ∠BAX]
And ∠APA4 = ∠BPB3 [Vertically opposite angle]
So, AA similarity criterion, we have
ΔAA4P ≈ ΔBB3P
`(A A_4)/(BB_3)=(AP)/(BP)`
`(AP)/(BP)=4/3`
APPEARS IN
संबंधित प्रश्न
Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5
Construct a triangle similar to a given ΔXYZ with its sides equal to (3/4)th of the corresponding sides of ΔXYZ. Write the steps of construction.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Choose the correct alternative:
ΔPQR ~ ΔABC, `"PR"/"AC" = 5/7`, then
Choose the correct alternative:
∆ABC ∼ ∆AQR. `"AB"/"AQ" = 7/5`, then which of the following option is true?
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
If the perpendicular distance between AP is given, which vertices of the similar triangle would you find first?
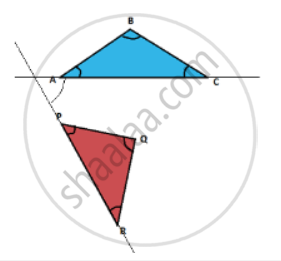
If you need to construct a triangle with point P as one of its vertices, which is the angle that you need to construct a side of the triangle?
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
Draw a line segment of length 7.5 cm and divide it in the ratio 1:3.
