Advertisements
Advertisements
प्रश्न
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
उत्तर
Steps of Construction:
Step 1: Draw a line segment AB = 7.6cm
Step 2: Draw a ray AX, making an acute angle ∠BAX.
Step 3: Along AX, mark (5+8 = )13points` A_1 , A_2 , A_3 , A_4 , A_5 , A_6 , A_7 , A_8 , A_9 , A_10 , A_11 , A_12 and
A_13` such that
`A A_1= A_1 A_2 = A_2 A_3 = A_3 A_4 = A_4 A_5 = A_6 A_7= A_8 A_9= A_9 A_10 = A_10 A_11 = A _11A_12 =A_12 A_13` .
Step 4: Join A13 B.
Step 5: From A5 , draw A5P parallel to A13B ( draw an angle equal to AA13 B ), meeting AB in P.
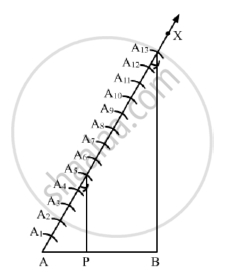
Here, P is the point on AB which divides it in the ratio 5 :8.
∴Length of AP = 2.9 cm (Approx)
Length of BP = 4.7 cm(Approx)
APPEARS IN
संबंधित प्रश्न
Find the ratio in which point T(–1, 6)divides the line segment joining the points P(–3, 10) and Q(6, –8).
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm, ∠D = 30°, ∠N = 20° and `"HP"/"ED" = 4/5`. Then construct ΔRHP and ΔNED
ΔABC ~ ΔPBR, BC = 8 cm, AC = 10 cm , ∠B = 90°, `"BC"/"BR" = 5/4` then construct ∆ABC and ΔPBR
When a line segment is divided in the ratio 2 : 3, how many parts is it divided into?
Construction of similar polygons is similar to that of construction of similar triangles. If you are asked to construct a parallelogram similar to a given parallelogram with a given scale factor, which of the given steps will help you construct a similar parallelogram?
A point C divides a line segment AB in the ratio 5 : 6. The ratio of lengths AB: BC is ______.

What is the ratio `(AC)/(BC)` for the line segment AB following the construction method below?
Step 1: A ray is extended from A and 30 arcs of equal lengths are cut, cutting the ray at A1, A2,…A30
Step 2: A line is drawn from A30 to B and a line parallel to A30B is drawn, passing through the point A17 and meet AB at C.
To construct a triangle similar to a given ∆ABC with its sides `7/3` of the corresponding sides of ∆ABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect to BC. The points B1, B2, ...., B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C where C' lies on BC produced. Finally, line segment A'C' is drawn parallel to AC.
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 9 cm. Construct a triangle similar to ∆ABC with scale factor `3/2`. Justify the construction. Are the two triangles congruent? Note that all the three angles and two sides of the two triangles are equal.
