Advertisements
Advertisements
Question
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Solution
Steps of Construction:
Step 1: Draw a line segment AB = 7.6cm
Step 2: Draw a ray AX, making an acute angle ∠BAX.
Step 3: Along AX, mark (5+8 = )13points` A_1 , A_2 , A_3 , A_4 , A_5 , A_6 , A_7 , A_8 , A_9 , A_10 , A_11 , A_12 and
A_13` such that
`A A_1= A_1 A_2 = A_2 A_3 = A_3 A_4 = A_4 A_5 = A_6 A_7= A_8 A_9= A_9 A_10 = A_10 A_11 = A _11A_12 =A_12 A_13` .
Step 4: Join A13 B.
Step 5: From A5 , draw A5P parallel to A13B ( draw an angle equal to AA13 B ), meeting AB in P.
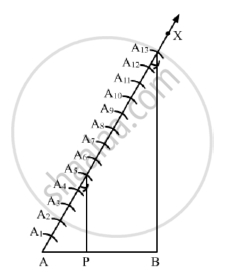
Here, P is the point on AB which divides it in the ratio 5 :8.
∴Length of AP = 2.9 cm (Approx)
Length of BP = 4.7 cm(Approx)
APPEARS IN
RELATED QUESTIONS
Construct a Δ ABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°, Construct another ΔAB’C’ similar to ΔABC with base AB’ = 8 cm.
Construct a triangle ABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another triangle whose sides are `2/3` times the corresponding sides of ΔABC.
Find the ratio in which point P(k, 7) divides the segment joining A(8, 9) and B(1, 2). Also find k.
Choose the correct alternative:
______ number of tangents can be drawn to a circle from the point on the circle.
Choose the correct alternative:

In the figure ΔABC ~ ΔADE then the ratio of their corresponding sides is ______
ΔAMT ~ ΔAHE. In ΔAMT, AM = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `"AM"/"HA" = 7/5`, then construct ΔAMT and ΔAHE
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm. ∠D = 30°, ∠N = 20°, `"HP"/"ED" = 4/5`, then construct ΔRHP and ∆NED
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
Draw a line segment of length 7.5 cm and divide it in the ratio 1:3.
