Advertisements
Advertisements
Question
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that `(AP)/(AB) = 3/5 `.
Solution
Steps of Construction:
Step 1: Draw a line segment AB = 7 cm
Step 2: Draw a ray AX, making an acute angle ∠BAX.
Step 3: Along AX, mark 5 points (greater of 3 and 5) `A^1 , A^2 , A^3 , A^4 and A^5` such that
`A A_1 = A_1 A_2 = A_ A_3 = A_3 A_4 = A_4 A_5`
Step 4: Join A5 B.
Step 5: From A3 , draw A3 P parallel to A5B ( draw an angle equal to 5 ∠AA5 B ), meeting AB in P.
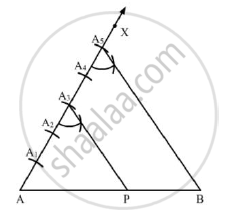
`"Here, P is the point on AB such that"(AP)/(PB) =3/2 or (AP)/(AB) = 3/5.`
APPEARS IN
RELATED QUESTIONS
Construct a triangle similar to a given ΔXYZ with its sides equal to (3/4)th of the corresponding sides of ΔXYZ. Write the steps of construction.
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are `3/5` times the corresponding sides of the given triangle.
If A(–14, –10), B(6, –2) is given, find the coordinates of the points which divide segment AB into four equal parts.
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm, ∠D = 30°, ∠N = 20° and `"HP"/"ED" = 4/5`. Then construct ΔRHP and ΔNED
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
Match the following based on the construction of similar triangles, if scale factor `(m/n)` is.
| Column I | Column II | ||
| i | >1 | a) | The similar triangle is smaller than the original triangle. |
| ii | <1 | b) | The two triangles are congruent triangles. |
| iii | =1 | c) | The similar triangle is larger than the original triangle. |
To construct a triangle similar to a given ∆ABC with its sides `7/3` of the corresponding sides of ∆ABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect to BC. The points B1, B2, ...., B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C where C' lies on BC produced. Finally, line segment A'C' is drawn parallel to AC.
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 9 cm. Construct a triangle similar to ∆ABC with scale factor `3/2`. Justify the construction. Are the two triangles congruent? Note that all the three angles and two sides of the two triangles are equal.
Draw a line segment AB of length 10 cm and divide it internally in the ratio of 2:5 Justify the division of line segment AB.
