Question

To construct a triangle similar to a given ∆ABC with its sides `7/3` of the corresponding sides of ∆ABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect to BC. The points B₁, B₂, ...., B₇ are located at equal distances on BX, B₃ is joined to C and then a line segment B₆C' is drawn parallel to B₃C where C' lies on BC produced. Finally, line segment A'C' is drawn parallel to AC.

Options

• True

• False

Answer 1

This statement is False.

Explanation:

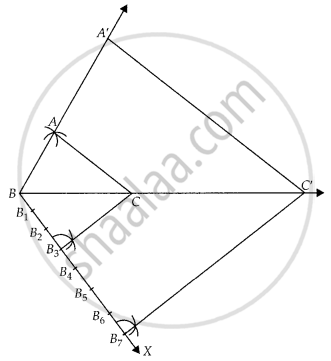
Steps of construction:

1. Draw a line segment BC.
2. With B and C as centres, draw two arcs of suitable radius intersecting each other at A.
3. Join BA and CA and we get the required triangle ∆ABC.
4. Draw a ray BX from B downwards to make an acute angle ∠CBX.
5. Now, mark seven points B₁, B₂, B₃ ... B₇ on BX, such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇.
6. Join B₃C and draw a line B₇C’ || B₃C from B₇ such that it intersects the extended line segment BC at C’.
7. Draw C’A’ || CA in such a way that it intersects the extended line segment BA at A’.

Then, ∆A’BC’ is the required triangle whose sides are `7/3` of the corresponding sides of ∆ABC.

According to the question,

We have,

Segment B₆C’ || B₃C.

But it is clear in our construction that it is never possible that segment B₆C’ || B₃C since the similar triangle A’BC’ has its sides `7/3` of the corresponding sides of triangle ABC.

So, B₇C’ is parallel to B₃C.