Advertisements
Advertisements
Question
Choose the correct alternative:
∆ABC ∼ ∆AQR. `"AB"/"AQ" = 7/5`, then which of the following option is true?
Options
A–Q–B
A–B–Q
A-C–B
A–R–B
Solution
A–Q–B
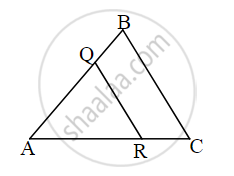
ΔABC ∼ ΔAQR and `"AB"/"AQ" = 7/5`
⇒ ΔABC is greater and ΔAQR is smaller.
∠A is a common angle.
∴ We get, A-Q-B
RELATED QUESTIONS
Construct a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60˚. Now construct another triangle whose sides are 5/7 times the corresponding sides of ΔABC.
Find the ratio in which the line segment joining the points A(3,- 3) and B(- 2, 7) is divided by x-axis. Also find the coordinates of the point of division.
Construct a triangle ABC in which BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are`3/4` times the corresponding sides of ΔABC.
Construct a triangle of sides 4 cm, 5cm and 6cm and then a triangle similar to it whose sides are `2/3` of the corresponding sides of the first triangle. Give the justification of the construction.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are `3/5` times the corresponding sides of the given triangle.
Determine a point which divides a line segment of length 12 cm internally in the ratio 2 : 3 Also, justify your construction.
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
Divide a line segment of length 14 cm internally in the ratio 2 : 5. Also, justify your construction.
Construct a triangle similar to a given ΔABC such that each of its sides is (2/3)rd of the corresponding sides of ΔABC. It is given that BC = 6 cm, ∠B = 50° and ∠C = 60°.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are 5/3th times the corresponding sides of the given triangle.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 3/2 times the corresponding sides of the isosceles triangle.
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° with scale factor 4 : 5.
Draw a right triangle in which sides (other than the hypotenuse) are of lengths 8 cm and 6 cm. Then construct another triangle whose sides are 3/4 times the corresponding sides of the first triangle.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Construct the circumcircle and incircle of an equilateral ∆XYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another triangle whose sides are `2/3` times the corresponding sides of ΔABC.
∆ABC ~ ∆LBN. In ∆ABC, AB = 5.1 cm, ∠B = 40°, BC = 4.8 cm, \[\frac{AC}{LN} = \frac{4}{7}\]. Construct ∆ABC and ∆LBN.
Find the ratio in which point P(k, 7) divides the segment joining A(8, 9) and B(1, 2). Also find k.
If A (20, 10), B(0, 20) are given, find the coordinates of the points which divide segment AB into five congruent parts.
Δ SHR ∼ Δ SVU. In Δ SHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and
SHSV = 53 then draw Δ SVU.
Choose the correct alternative:

In the figure ΔABC ~ ΔADE then the ratio of their corresponding sides is ______
Choose the correct alternative:
ΔPQR ~ ΔABC, `"PR"/"AC" = 5/7`, then
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm, ∠D = 30°, ∠N = 20° and `"HP"/"ED" = 4/5`. Then construct ΔRHP and ΔNED
Construct an equilateral ∆ABC with side 5 cm. ∆ABC ~ ∆LMN, ratio the corresponding sides of triangle is 6 : 7, then construct ΔLMN and ΔABC
ΔABC ~ ΔPBR, BC = 8 cm, AC = 10 cm , ∠B = 90°, `"BC"/"BR" = 5/4` then construct ∆ABC and ΔPBR
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
To construct a triangle similar to a given ΔABC with its sides `8/5` of the corresponding sides of ΔABC draw a ray BX such that ∠CBX is an acute angle and X is on the opposite side of A with respect to BC. Then minimum number of points to be located at equal distances on ray BX is ______.
For ∆ABC in which BC = 7.5cm, ∠B =45° and AB - AC = 4, select the correct figure.
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

The point W divides the line XY in the ratio m : n. Then, the ratio of lengths of the line segments XY : WX is ______.
What is the ratio `(AC)/(BC)` for the line segment AB following the construction method below?
Step 1: A ray is extended from A and 30 arcs of equal lengths are cut, cutting the ray at A1, A2,…A30
Step 2: A line is drawn from A30 to B and a line parallel to A30B is drawn, passing through the point A17 and meet AB at C.
To construct a triangle similar to a given ∆ABC with its sides `7/3` of the corresponding sides of ∆ABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect to BC. The points B1, B2, ...., B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C where C' lies on BC produced. Finally, line segment A'C' is drawn parallel to AC.
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
Draw a right triangle ABC in which BC = 12 cm, AB = 5 cm and ∠B = 90°. Construct a triangle similar to it and of scale factor `2/3`. Is the new triangle also a right triangle?
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
Draw a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Construct a triangle similar to ∆ABC with scale factor `5/7`. Justify the construction.
