Advertisements
Advertisements
Question
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are 5/3th times the corresponding sides of the given triangle.
Solution
Given that
Construct a right triangle of sides let AB = 5cm, AC = 4cm and ∠A = 90° and then a triangle similar to it whose sides are 5/3th of the corresponding sides of .
We follow the following steps to construct the given
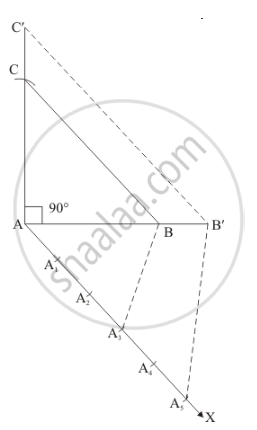
Step of construction
Step: I- First of all we draw a line segment AB = 5cm.
Step: II- With A as centre and draw an angle ∠A = 90°.
Step: III- With A as centre and radius AC = 4cm.
Step: IV -Join BC to obtain ΔABC.
Step: V -Below AB, makes an acute angle ∠BAX = 60°.
Step: VI -Along AX, mark off five points A1, A2, A3, A4 and A5 such that AA1 = A1A2 = A2A3 = A3A4 = A4A5
Step: VII -Join A3B.
Step: VIII -Since we have to construct a triangle each of whose sides is 5/3th of the corresponding sides of ΔABC.
So, we draw a line A5B on AX from point A5 which is A5B' || A3B, and meeting AB at B’.
Step: IX -From B’ point draw B'C' || BC, and meeting AC at C’
Thus, ΔAB'C' is the required triangle, each of whose sides is 5/3th of the corresponding sides of ΔABC.
APPEARS IN
RELATED QUESTIONS
ΔRST ~ ΔUAY, In ΔRST, RS = 6 cm, ∠S = 50°, ST = 7.5 cm. The corresponding sides of ΔRST and ΔUAY are in the ratio 5 : 4. Construct ΔUAY.
Construct a triangle similar to a given ΔXYZ with its sides equal to (3/4)th of the corresponding sides of ΔXYZ. Write the steps of construction.
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that `(AP)/(AB) = 3/5 `.
Draw a ∆ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Then construct another triangle whose sides are\[\frac{3}{5}\] of the corresponding sides of ∆ABC ?
Given A(4, –3), B(8, 5). Find the coordinates of the point that divides segment AB in the ratio 3 : 1.
Find the co-ordinates of the centroid of the Δ PQR, whose vertices are P(3, –5), Q(4, 3) and R(11, –4)
If I ask you to construct ΔPQR ~ ΔABC exactly (when we say exactly, we mean the exact relative positions of the triangles) as given in the figure, (Assuming I give you the dimensions of ΔABC and the Scale Factor for ΔPQR) what additional information would you ask for?
Match the following based on the construction of similar triangles, if scale factor `(m/n)` is.
| Column I | Column II | ||
| i | >1 | a) | The similar triangle is smaller than the original triangle. |
| ii | <1 | b) | The two triangles are congruent triangles. |
| iii | =1 | c) | The similar triangle is larger than the original triangle. |
Construction of similar polygons is similar to that of construction of similar triangles. If you are asked to construct a parallelogram similar to a given parallelogram with a given scale factor, which of the given steps will help you construct a similar parallelogram?
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
