Advertisements
Advertisements
प्रश्न
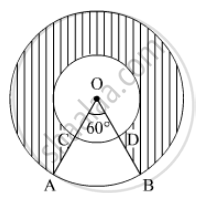
In Figure , two concentric circles with centre O, have radii 21cm and 42 cm. If ∠ AOB = 60°, find the area of the shaded region. [use π=22/7]
उत्तर १
Solution:
Given :
Radii of inner circle = 21 cm = r
Radii of outer circle = 42 cm = R
∠AOB = θ = 60°
Also,
Area of ring = π(R2-r2)
Area of a sector `= theta/360 pir^2`
The area of shaded region = Area of ring – Area of ABCD
= Area of ring – Area of sector of Outer Circle - Area of sector of Inner Circle
`=pi(R^2-r^2)-(pi(R^2-r^2))/1 xx theta/360`
`=pi(R^2-r^2)[1-theta/360]`
`=22/7(42^2-21^2)(1-60/360)`
`=3465 cm^2`
उत्तर २
Solution:
Given :
Radii of inner circle = 21 cm = r
Radii of outer circle = 42 cm = R
∠AOB = θ = 60°
Also,
Area of ring = π(R2-r2)
Area of a sector `= theta/360 pir^2`

The area of shaded region = Area of ring – Area of ABCD
= Area of ring – Area of sector of Outer Circle - Area of sector of Inner Circle
`=pi(R^2-r^2)-(pi(R^2-r^2))/1 xx theta/360`
`=pi(R^2-r^2)[1-theta/360]`
`=22/7(42^2-21^2)(1-60/360)`
`=3465 cm^2`
उत्तर ३
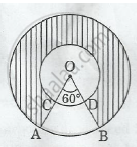
Given: Radius of the inner circle with radius OC, r = 21 cm
Radius of the inner circle with radius OA, R = 42 cm
∠AOB = 60°
Area of the circular ring
`= piR^2 - pir^2`
`=pi[R^2 - r^2]`
`=pi[42^2 - 21^2] cm^2`
Area of ACDB = area of sector AOB − area of COD
`= 60/360 xx pi xx R^2 - 60/300 xx pi xx r^2`
`= 60/360 xx pi[R^2 - r^2]`
`= 60/360 xx pi[42^2 - 21^2]`
Area of shaded region = area of circular ring − area of ACDB
`= pi[42^2 - 21^2] - 60/360 pi [42^2 - 21^2]`
`= pi[42^2 - 21^2][1 - 60/360]`
`= 22/7 (42 - 21) (42 + 21) xx 300/360`
`=3465 cm^2`
APPEARS IN
संबंधित प्रश्न
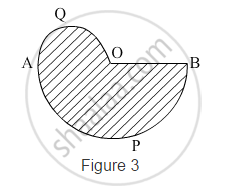
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. Find:
(i) the total length of the silver wire required
(ii) the area of each sector of the brooch
Find the angle subtended at the centre of circle of radius 5cm by an arc of length `((5pi)/3)` cm
An arc of length 20𝜋 cm subtends an angle of 144° at centre of circle. Find the radius of the circle.
The minute hand of a clock is √21 𝑐𝑚 long. Find area described by the minute hand on the face of clock between 7 am and 7:05 am
A square water tank has its side equal to 40m, there are 4 semicircular flower beds grassy plots all around it. Find the cost of turfing the plot at Rs 1.25/sq.m
The areas of two circles are in the ratio 4: 9. What is the ratio between their circumferences?
Find the area and perimeter of the following sector :
Diameter = 42 cm, angle at the centre is 100·.
The diameter of a circular well is 4.2 m. What is its circumference?
The distance around a circle is its ______.
