Advertisements
Advertisements
Question
Find the area and perimeter of the following semicircles: Diameter = 7cm
Solution
The radius of a Circle with diameter d is r = `"d"/(2)`
The Area of a Semi-circle with radius r = `(pi"r"^2)/(2)`
The Perimeter of a Semi-circle with radius r
= πr + 2r
= r(π + 2)
= `"r"(22/7 + 2)`
= `(36)/(7) xx "r"`
The radius of a Circle with diameter 7 is r
= `(7)/(2)`
= 3.5cm
The Area of a Semi-circle with radius 3.5
= `(pi(3.5)^2)/(2)`
= 19.25cm2
The Perimeter of a Semi-circle with radius r
= π x 3.5 + 2 x 3.5
= 3.5(π + 2)
= `3.5(22/7 + 2)`
= `(36)/(7) xx 3.5`
= 25cm.
APPEARS IN
RELATED QUESTIONS
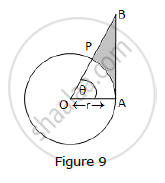
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
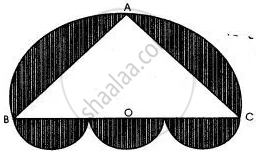
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)
The areas of two circles are in the ratio 4: 9. What is the ratio between their circumferences?
The diameter of a wheel is 1.4m. How many revolutions does it make in moving a distance of 2.2 kms?
Find the volume and the surface area of the spheres in the following :
Radius= 2.1 cm
An express train is running between two stations with a uniform speed. If the diameter of each wheel of the train is 42 cm and each wheel makes 1200 revolutions per minute, find the speed of the train.
Find the radius of the circle whose circumference is equal to the sum of the circumferences of the circles having radius 15 cm and 8 cm.
A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/sec, calculate the number of complete revolutions the wheel makes in raising the bucket. (Take π =22/7)
The area of a square is 100 cm2. The circumference (in cm) of the largest circle cut of it is ______.
The moon is about 384000 km from earth and its path around the earth is nearly circular. Find the length of path described by moon in one complete revolution. (Take π = 3.14)
